C++ 中的灯泡切换器 III
c++server side programmingprogramming
假设我们有一个房间里有 n 个灯泡,这些灯泡从 1 到 n 编号,从左到右排成一行。最初,所有灯泡都关闭。在时刻 k(k 在 0 到 n - 1 的范围内),我们打开 light[k] 灯泡。只有当灯泡打开并且所有先前的灯泡(左侧)也打开时,灯泡才会变为蓝色。我们必须找出所有打开的灯泡都是蓝色的时刻数。所以这是一个例子 −
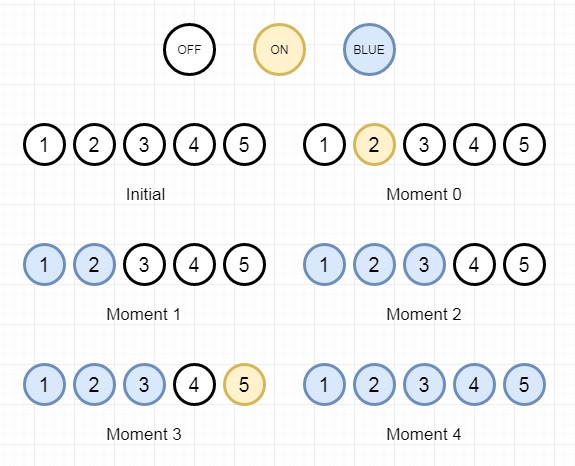
由于矩为 1、2 和 4,因此输出将为 3。
为了解决这个问题,我们将遵循以下步骤 −
ret := 0,定义一个集合 x,n := 列表数组的大小,定义一个映射 m
定义一个基于堆的最大优先级队列 pq
对于 I 在 0 到 n 的范围内 – 1
m[light[i]] := i 并将 i 插入 pq
对于范围为 1 到 n 的 I
将 m[i] 插入 x
当 pq 不为空且 pq 的顶部元素在集合 x 中时,
从 pq 中删除
当 (pq 为空或 pq 的顶部 >= i) 时,ret := ret + 1,否则为 0
return res
示例 (C++)
让我们看下面的实现,以便更好地理解 −
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int numTimesAllBlue(vector<int>& light) {
int ret = 0;
set <int> x;
int n = light.size();
map <int, int> m;
priority_queue <int, vector <int>, greater <int> > pq;
for(int i = 0; i < n; i++){
m[light[i]] = i;
pq.push(i);
}
for(int i = 1; i <=n; i++){
x.insert(m[i]);
while(!pq.empty() && x.count(pq.top()))pq.pop();
ret += (pq.empty() || (pq.top() >= i));
}
return ret;
}
};
main(){
vector<int> v = {2,1,3,5,4};
Solution ob;
cout << (ob.numTimesAllBlue(v));
}
输入
[2,1,3,5,4]
输出
3


