在 C++ 中计算位于给定范围内的 BST 节点数
c++server side programmingprogramming更新于 2024/9/27 8:06:00
我们给定一个由节点和一个范围组成的二叉搜索树，任务是计算位于给定范围内的节点数并显示结果。
二叉搜索树 (BST) 是一棵树，其中所有节点都遵循以下属性 −
节点的左子树的键小于或等于其父节点的键。
节点的右子树的键大于其父节点的键。
因此，BST 将其所有子树分为两部分；左子树和右子树，可以定义为 −
left_subtree (keys) ≤ node (key) ≤ right_subtree (keys)
例如
输入 −
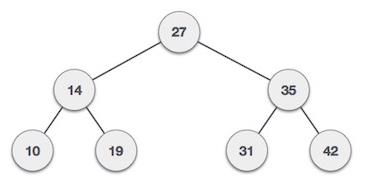
范围:[11, 40]
输出 − 计数为:5
解释 −范围 [11, 40] 之间的节点值为 14、19、27、31 和 35，因此给定的二叉搜索树中总共有 5 个节点。
以下程序中使用的方法如下
创建一个包含数据、左指针、右指针的节点结构并创建一个范围
创建一个函数来插入用户将输入的新节点。
创建另一个函数来计算位于给定范围内的节点数。
检查根是否为 NULL，然后返回
现在，检查根->data = Start 和根->data = End，然后返回 1。
现在，检查根->data <= high && root->data >= low 然后返回 1 + getCount(root->left, End, Start) + recursively_call_count_function(root->right, End, Start)
否则，如果 root->data < End 然后返回 recursively_call_count_function(root->right, End, Start)
否则，返回 recursively_call_count_function(root->left, End, Start)
示例
#include<iostream>
using namespace std;
// BST 节点
struct node{
int data;
struct node* left, *right;
};
// 创建新节点的实用函数
node *newNode(int data){
node *temp = new node;
temp->data = data;
temp->left = temp->right = NULL;
return (temp);
}
int findcount(node *root, int low, int high){
// 基本情况
if (!root){
return 0;
}
if (root->data == high && root->data == low){
return 1;
}
// 如果当前节点在范围内，则将其包含在计数中
// 对其左子节点和右子节点进行递归
if (root->data <= high && root->data >= low){
return 1 + findcount(root->left, low, high) +
findcount(root->right, low, high);
}
else if (root->data < low){
return findcount(root->right, low, high);
}
// 否则对左节点进行递归
else{
return findcount(root->left, low, high);
}
}
// main 主函数
int main(){
// 让我们构造上图所示的 BST
node *root = newNode(27);
root->left = newNode(14);
root->right = newNode(35);
root->left->left = newNode(10);
root->left->right = newNode(19);
root->right->left = newNode(31);
root->right->right = newNode(42);
int low = 10;
int high = 50;
cout << "Count of nodes between [" << low << ", " << high
<< "] is " << findcount(root, low, high);
return 0;
}
输出
如果运行上述代码，我们将得到以下输出 −
Count of nodes between [10, 50] is 7
