使用 C++ 计算二叉树中最大值根
c++server side programmingprogramming更新于 2024/9/28 3:04:00
假设我们有一个二叉树根;我们必须计算其值大于或等于其所有后代值的节点数。
因此,如果输入如下
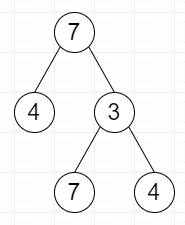
则输出将为 4,因为除 3 之外的所有节点都符合条件。
为了解决这个问题,我们将遵循以下步骤 −
定义一个函数 dfs(),它将接受节点,
如果节点不为空,则 −
返回 0
l := dfs(节点左侧)
r := dfs(节点右侧)
如果节点值 >= l 和 r 的最大值,则 −
(将 ret 增加 1)
x := 节点、l 和 r 值之和的最大值
返回 x
从主方法中,执行以下操作,
ret := 0
dfs(root)
return ret
让我们看看下面的实现以便更好地理解 −
示例
#include <bits/stdc++.h>
using namespace std;
class TreeNode {
public:
int val;
TreeNode *left, *right;
TreeNode(int data) {
val = data;
left = NULL;
right = NULL;
}
};
class Solution {
public:
int ret;
int dfs(TreeNode* node){
if(!node)
return 0;
int l = dfs(node->left);
int r = dfs(node->right);
if(node->val >= max(l, r)) {
ret++;
}
int x = max({node->val, l, r});
return x;
}
int solve(TreeNode* root) {
ret = 0;
dfs(root);
return ret;
}
};
main(){
Solution ob;
TreeNode *root = new TreeNode(7);
root->left = new TreeNode(4);
root->right = new TreeNode(3);
root->right->left = new TreeNode(7);
root->right->right = new TreeNode(5);
cout << (ob.solve(root));
}
输入
TreeNode *root = new TreeNode(7); root->left = new TreeNode(4); root->right = new TreeNode(3); root->right->left = new TreeNode(7); root->right->right = new TreeNode(5);
输出
4

