二分法 C++ 程序
c++server side programmingprogramming更新于 2024/10/5 3:46:00
给定函数 f(x),其值为 a 和 b,其中 f(a) * f(b) > 0,且函数 f(x) 应位于 a 和 b 之间,即 f(x) = [a, b]。任务是使用二分法找到函数 f(x) 中位于区间 a 和 b 之间的根值。
什么是二分法?
二分法用于在由"a"和"b"定义的给定限制内找到函数 f(x) 中根的值。函数的根可以定义为值 a,使得 f(a) = 0。
示例
二次方程 F(x) = - 8 当 x 的值为 2 时,此方程等于 0,即 - 8 = 0 因此,此二次函数 F(x) 的根为 2。
现在,如果函数 f(x) 在给定区间 [a..b] 内连续,并且 f(a) 的符号 &f(b) 的符号为 n,则将有一个值 m 属于区间 a 和 b,使得 f(m) = 0
值 m [a..b],使得 f(m) = 0
即m 是根的值,可以是多个
下图显示了区间 f(a) 和 f(b)。为了找到这些区间之间的根,将极限分成几部分并存储在变量 m 中,即
m = (a + b) / 2
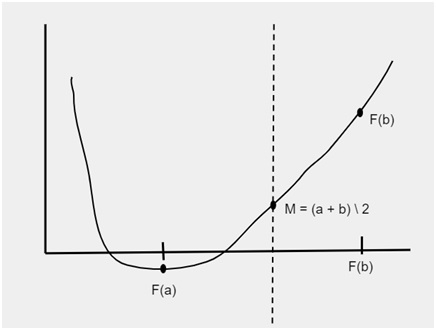
极限划分后,将生成新的区间,如下图所示
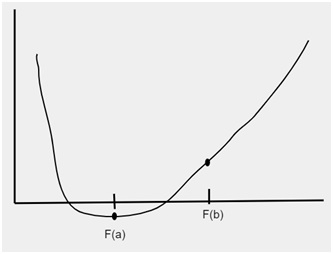
示例
输入:x^3 - x^2 + 2 ; a =-500 和 b = 100 输出:根的值为:-0.991821 输入:x^3 - x^2 + 2 ; a =-200 和 b = 300 输出:根的值为:-1.0025
我们在以下程序中使用的方法如下 −
- 输入方程以及区间 a 和 b 的值
- 将区间除以 :m = (a + b) / 2
- 打印 m 是根
- 如果 f(m) ≠ 0
- 检查 f(a) * f(m) 是否 < 0
- 则根将位于 a 和 m 之间
- 检查 f(b) * f(m) 是否 < 0
- 则根将位于 b 和 m 之间
算法
开始 步骤 1-> 在函数 double solution(double x) 中 返回 x*x*x - x*x + 2 步骤 2-> 在函数 bisection(double a, double b) 中 如果 solution(a) * solution(b) >= 0,则 打印 "您没有假设正确的 a 和 b" 返回 结束如果 设置 c = a 循环 While (b-a) >= EP 设置 c = (a+b)/2 如果解决方案(c)== 0.0 中断 如果结束 否则如果解决方案(c)*解决方案(a)< 0 设置 b = c 结束否则如果 否则 设置 a = c 结束否则 结束 打印"根的值" 步骤 3-> 在函数 int main() 中 声明并初始化输入 a =-500, b = 100 调用函数 bisection(a, b) 停止
示例
#include <iostream>
using namespace std;
#define EP 0.01
// 示例函数,其解使用
// 二分法确定。该函数为 x^3 - x^2 + 2
double solution(double x) {
return x*x*x - x*x + 2;
}
// 打印带有 EPSILON 错误的解 (x) 的根
void bisection(double a, double b) {
if (solution(a) * solution(b) >= 0) {
cout << "您没有假设正确的 a 和 b\n";
return;
}
double c = a;
while ((b-a) >= EP) {
// 找到中间点
c = (a+b)/2;
// 检查中间点是否为根
if (solution(c) == 0.0)
break;
// 决定重复步骤的一侧
else if (solution(c)*solution(a) < 0)
b = c;
else
a = c;
}
cout << "root 的值为 : " << c;
}
// main 主函数
int main() {
double a =-500, b = 100;
bisection(a, b);
return 0;
}
输出
root 的值为:-0.991821

