C++ 中的多米诺骨牌和特罗米诺骨牌平铺
c++server side programmingprogramming更新于 2024/11/8 22:20:00
假设我们有两种形状,多米诺骨牌和特罗米诺骨牌。它们可以像下面这样旋转 −
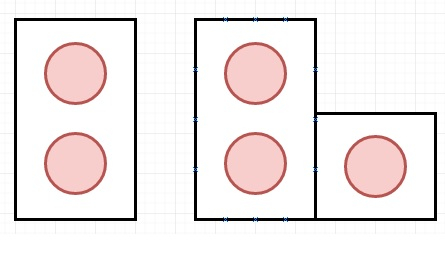
在平铺中,每个方块都必须被一个方块覆盖。当且仅当棋盘上有两个 4 方向相邻的单元格,并且恰好其中一个平铺的两个方块都被一个方块占据时,两个平铺才会不同。
给定 N,那么我们必须找出有多少种平铺 2xN 棋盘的方法?因此,如果输入为 3,则输出将为 5。因此排列可以是 [XYZ XXZ XYY XXY XYY] 和 [XYZ YYZ XZZ XYY XXY],这里不同的字母用于不同的图块。
为了解决这个问题,我们将遵循以下步骤 −
创建一个名为 dp 的数组,大小为 N + 5,设置 dp[1] := 1、dp[2] := 2 和 dp[3] := 5
for i in range 4 to N
dp[i] := 2*dp[i – 1] + dp[i – 3]
return dp[N]
示例(C++)
让我们看下面的实现,以便更好地理解 −
#include <bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7;
int add(int a, int b){
return ((a % MOD) + (b % MOD)) % MOD;
}
class Solution {
public:
int numTilings(int N) {
vector <int> dp(N + 5);
dp[1] = 1;
dp[2] = 2;
dp[3] = 5;
for(int i = 4; i <= N; i++){
dp[i] = add(2 * dp[i - 1], dp[i - 3]);
}
return dp[N];
}
};
main(){
Solution ob;
cout << (ob.numTilings(3));
}
输入
3
输出
5

