在 C++ 程序中查找二叉树两个节点之间的距离
c++server side programmingprogramming更新于 2025/3/8 15:07:17
在这个问题中,我们给出了一棵二叉树和两个节点。我们的任务是创建一个程序来查找二叉树两个节点之间的距离。
问题描述
我们需要找到两个节点之间的距离,即从一个节点到另一个节点时将遍历的最小边数。
让我们举一个例子来理解这个问题,
输入:二叉树
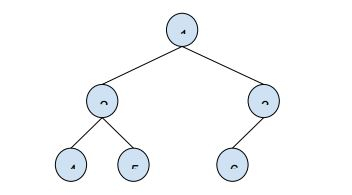
Node1 = 3,Node2 = 5
输出: 3
解释
从节点 3 到节点 5 的路径为 3 -> 1 -> 2 -> 5。遍历了 3 条边,距离为 3。
解决方法
该问题的一个简单解决方案是使用给定节点的最低公共祖先节点,然后应用以下公式,
distance(node1, node2) = distance(root, node1) + distance(root, node2) + distance(root, LCA)
示例
#include <iostream>
using namespace std;
struct Node{
struct Node *left, *right;
int key;
};
Node* insertNode(int key){
Node *temp = new Node;
temp->key = key;
temp->left = temp->right = NULL;
return temp;
}
int calcNodeLevel(Node *root, int val, int level) {
if (root == NULL)
return -1;
if (root->key == val)
return level;
int lvl = calcNodeLevel(root->left, val, level+1);
return (lvl != -1)? lvl : calcNodeLevel(root->right, val, level+1);
}
Node *findDistanceRec(Node* root, int node1, int node2, int &dist1, int &dist2, int &dist, int lvl){
if (root == NULL) return NULL;
if (root->key == node1){
dist1 = lvl;
return root;
}
if (root->key == node2){
dist2 = lvl;
return root;
}
Node *leftLCA = findDistanceRec(root->left, node1, node2, dist1,dist2, dist, lvl+1);
Node *rightLCA = findDistanceRec(root->right, node1, node2, dist1,dist2, dist, lvl+1);
if (leftLCA && rightLCA){
dist = dist1 + dist2 - 2*lvl;
return root;
}
return (leftLCA != NULL)? leftLCA: rightLCA;
}
int CalcNodeDistance(Node *root, int node1, int node2) {
int dist1 = -1, dist2 = -1, dist;
Node *lca = findDistanceRec(root, node1, node2, dist1, dist2, dist, 1);
if (dist1 != -1 && dist2 != -1)
return dist;
if (dist1 != -1){
dist = calcNodeLevel(lca, node2, 0);
return dist;
}
if (dist2 != -1){
dist = calcNodeLevel(lca, node1, 0);
return dist;
}
return -1;
}
int main(){
Node * root = insertNode(1);
root->left = insertNode(2);
root->right = insertNode(3);
root->left->left = insertNode(4);
root->left->right = insertNode(5);
root->right->left = insertNode(6);
cout<<"值为 5 的节点与值为 3 的节点之间的距离为"<<CalcNodeDistance(root, 3, 5);
return 0;
}
输出
值为 5 的节点与值为 3 的节点之间的距离为 3

