在 C++ 中查找距离阈值处邻居数量最少的城市
c++server side programmingprogramming
假设有 n 个城市，编号从 0 到 n-1。如果我们有数组 edge，其中 edge[i] = [fromi, toi, weighti] 表示城市 fromi 和 toi 之间的双向加权边，并给定整数距离阈值。我们必须找到可通过某条路径到达且距离最多为距离阈值的城市数量最少的城市，如果有多个这样的城市，则返回数量最多的城市。
因此，如果输入像 −
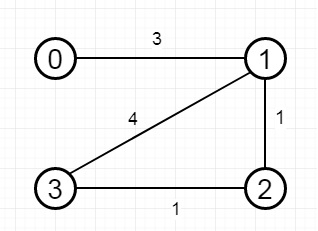
n 为 4，距离阈值也为 4，则输出为 3。这是因为 −
每个城市距离阈值 = 4 处的邻近城市为 −
C0 -> [C1, C2] C1 -> [C0, C2, C3] C2 -> [C0, C1, C3] C3 -> [C1, C2]
城市 0 和 3 在距离阈值 = 4 处有 2 个邻近城市，但我们必须返回城市 3，因为它的数字最大。
为了解决这个问题，我们将遵循以下步骤 −
定义一个 n x n 阶方阵，称为 dp，并用无穷大填充
生成图的邻接矩阵(成本矩阵)并存储到 dp 中
ret := 0 and cnt := infinity
for k in range 0 to n – 1
for i in range 0 to n – 1
for j in range 0 to n – 1
如果 i = j，则进行下一次迭代
如果 dp[i, j] > dp[i, k] + dp[k, j]，则
dp[j, i] := dp[i, k] + dp[k, j]
dp[i, j] := dp[i, k] + dp[k, j]
对于 i 在 0 到 n - 1 范围内
temp := 0
对于 j 在 0 到 n – 1 范围内
当 dp[i, j] <= t 时，temp := temp + 1，否则 temp 保持不变
如果 temp <= cnt，则 cnt := temp 且 ret := i
return ret
示例 (C++)
让我们看看下面的实现以便更好地理解 −
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int findTheCity(int n, vector<vector<int>>& e, int t) {
vector < vector <int> > dp(n, vector <int>(n, 1e7));
for(int i = 0; i < e.size(); i++){
int u = e[i][0];
int v = e[i][1];
int w = e[i][2];
dp[u][v] = w;
dp[v][u] = w;
}
int ret = 0;
int cnt = INT_MAX;
for(int k = 0; k < n; k++){
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
if(i == j) continue;
if(dp[i][j] > dp[i][k] + dp[k][j]){
dp[j][i] = dp[i][j] = (dp[i][k] + dp[k][j]);
}
}
}
}
for(int i = 0; i < n; i++){
int temp = 0;
for(int j = 0; j < n; j++){
temp += (dp[i][j] <= t);
}
if(temp <= cnt){
cnt = temp;
ret = i;
}
}
return ret;
}
};
main(){
vector<vector<int>> v = {{0,1,3},{1,2,1},{1,3,4},{2,3,1}};
Solution ob;
cout << (ob.findTheCity(4, v, 4));
}
输入
4 [[0,1,3],[1,2,1],[1,3,4],[2,3,1]] 4
输出
3
