使用 Python 进行高斯拟合
如今,数据分析和可视化至关重要,数据是新的石油。通常,数据分析涉及将数据输入数学模型并提取有用信息。高斯拟合是一种强大的数学模型,数据科学家使用它根据钟形曲线对数据进行建模。在本文中,我们将了解高斯拟合以及如何使用 Python 对其进行编码。
什么是高斯拟合
钟形曲线表征高斯分布。钟形曲线围绕均值 (μ) 对称。我们定义一个概率密度函数如下
f(x) = (1 / (σ * sqrt(2π))) * exp(-(x - μ)² / (2 * σ²))
这里 σ 表示分布的标准差,μ 是平均值,π (pie) 是常数,其值约为 3.14。
我们必须估计 μ 和 σ 的值才能将任何数据拟合到高斯分布中。手动执行此任务或创建逻辑代码会很繁琐且不方便。因此,Python 为我们提供了一些内置库和函数来处理它。
钟形曲线
钟形曲线是通过高斯分布获得的图。在进一步了解之前,读者需要了解钟形曲线的典型形状。这将为读者在将来处理高斯分布时提供更好的直观感受。
示例代码
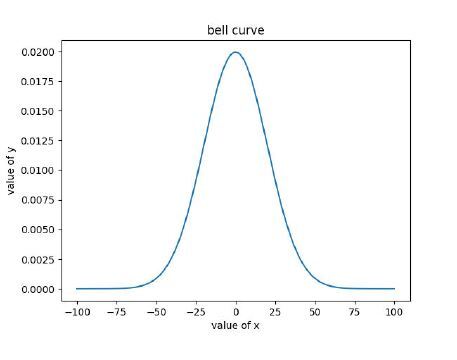
在下面的代码中,我们使用 Numpy 的arrange函数生成了一个统一的数据点。我们使用norm.pdf函数来计算高斯分布的概率分布函数。我们传入25作为均值,标准差为25。我们使用matplotlib库绘制了概率分布函数。从图中可以观察到的一个重要现象是,0附近的值比-100和100等极端值更常见。
import numpy as np
import scipy as sp
from scipy import stats
import matplotlib.pyplot as plt
x_data = np.arange(-100, 100, 0.01)
y_data = stats.norm.pdf(x_data, 25, 20)
plt.plot(x_data, y_data)
plt.title("bell curve")
plt.xlabel("value of x")
plt.ylabel("value of y")
plt.show()
输出
如何使用 curve_fit 方法
正如我们在上一节中讨论的那样,拟合高斯分布的主要思想是找到 μ 和 σ 的最优值。因此,我们可以执行以下算法来实现相同的目的。
首先,定义高斯函数。我们可以自己编写如下代码
def gaussian(x, μ, σ): return (1 / (σ * np.sqrt(2 * np.pi))) * np.exp(-((x - μ) ** 2) / (2 * σ ** 2))
借助 SciPy 包中的 curve_fit 方法执行高斯拟合。该方法返回 μ 和 σ 的最佳参数。
接下来,通过生成 y 值并使用任何标准数据可视化库(如 Matplotlib)来生成图
示例
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
def gaussian(x, μ, σ):
return (1 / (σ * np.sqrt(2 * np.pi))) * np.exp(-((x - μ) ** 2) / (2 * σ** 2))
x_data = np.linspace(-5, 5, 100)
y_data = gaussian(x_data, 0, 1) + np.random.normal(0, 0.2, 100)
popt, pcov = curve_fit(gaussian, x_data, y_data)
μ_fit, σ_fit = popt
y_fit = gaussian(x_data, μ_fit, σ_fit)
plt.scatter(x_data, y_data, label='Data')
plt.plot(x_data, y_fit, 'r', label='Fit')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
输出
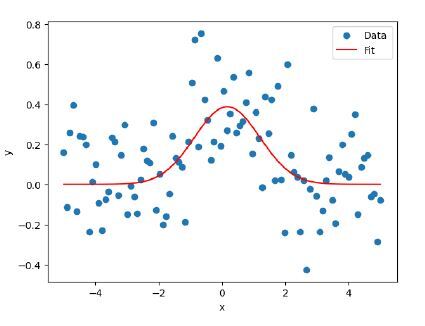
注意 - 由于我们生成随机数,因此每次生成的输出都会有所不同
结论
在本文中,我们了解了如何在 Python 中执行高斯拟合。这是一种处理钟形分布曲线的宝贵技术。幸运的是,python 为我们提供了标准库,我们可以使用这些库将数据拟合到高斯分布模型。我们建议读者在更多数据集上尝试分布,以对该主题更有信心。

