如何在 Python 中创建泊松概率质量函数图?
泊松分布是一种概率分布,它根据平均发生率对固定时间或空间间隔内事件的发生进行建模。它通常用于物理、工程和经济学等领域,以模拟粒子的到达、组件的故障或客户的到达。
可视化泊松分布的一种方法是绘制其概率质量函数 (PMF),它显示了给定间隔内每个可能事件数量的概率。在 Python 中,我们可以使用 SciPy 库生成泊松分布的 PMF,然后使用 Matplotlib 绘制它。
在本文中,我们将探讨如何使用 SciPy 和 Matplotlib 在 Python 中创建泊松 PMF 图。我们将为泊松参数的不同值生成 PMF,并使用条形图可视化结果。
现在让我们讨论一下我们可以用来创建泊松概率质量函数的不同方法。
使用 Scipy 库:Scipy 是一个流行的科学计算库,其中包括用于生成和可视化概率分布的函数。
使用 NumPy 和 Matplotlib:NumPy 是一个用于 Python 科学计算的库,其中包括用于生成随机数数组的函数。
在本文中,我们将借助示例讨论这两种方法。
使用 scipy 库
考虑下面显示的代码。
示例
import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt
# 设置泊松参数和 k 值的范围
lam = 2
k_values = np.arange(0, 11)
# 使用 Scipy 库计算 PMF
pmf_values = poisson.pmf(k_values, lam)
# 使用 Matplotlib 绘制 PMF
plt.plot(k_values, pmf_values, 'bo-', linewidth=2)
plt.xlabel('Number of events')
plt.ylabel('Probability')
plt.title('Poisson PMF (lambda=2)')
plt.grid(True)
plt.show()
解释
我们首先导入必要的库:NumPy、Scipy 和 Matplotlib。
我们将泊松参数 lambda 设置为 2,它定义了泊松分布中事件发生的速率。
我们将 k 值的范围定义为 0 到 10,代表事件的数量。
我们使用 Scipy 库中的 poisson.pmf() 函数来计算给定 lambda 和 k 值的 PMF 值。
我们使用 plt.plot() 函数绘制 PMF 值来自 Matplotlib,以蓝色圆圈 ('bo-') 作为标记,线宽为 2。我们还为图的 x 轴、y 轴和标题添加标签,以及网格以帮助可视化。
最后,我们使用 plt.show() 函数显示图。
要运行下面显示的代码,我们首先需要安装 scipy 库,为此我们可以运行下面显示的命令。
命令
pip3 install scipy
现在运行下面显示的命令。
python3 main.py
输出
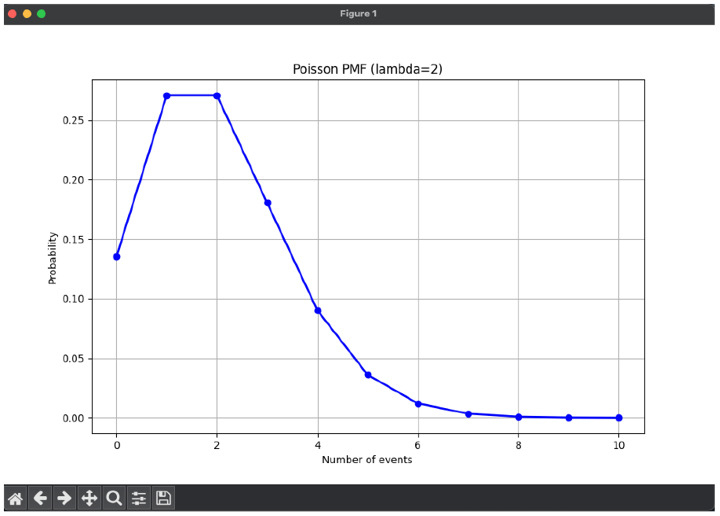
使用 numPy 和 Matplotlib
考虑下面显示的代码。
示例
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# 定义泊松分布参数 lambda
lam = 3
# 创建 x 值数组
x = np.arange(0, 15).tolist()
# 创建泊松概率质量函数
pmf = poisson.pmf(x, lam)
# 创建图
plt.plot(x, pmf, 'bo', ms=8)
plt.vlines(x, 0, pmf, colors='b', lw=5)
plt.title('Poisson Probability Mass Function')
plt.xlabel('Number of events')
plt.ylabel('Probability')
plt.show()
说明
代码首先导入必要的库,包括 NumPy 和 Matplotlib。
定义 lambda 函数来计算泊松分布的概率质量函数。
设置 lambda 的值和 k 值的范围。
使用先前定义的 lambda 函数,使用 lambda 值和 k 范围计算概率质量函数。
使用 Matplotlib 库,使用 k 和概率值创建线图。
设置 x 和 y 轴标签,并为图定义标题。
show() 方法被调用来显示图表。
输出
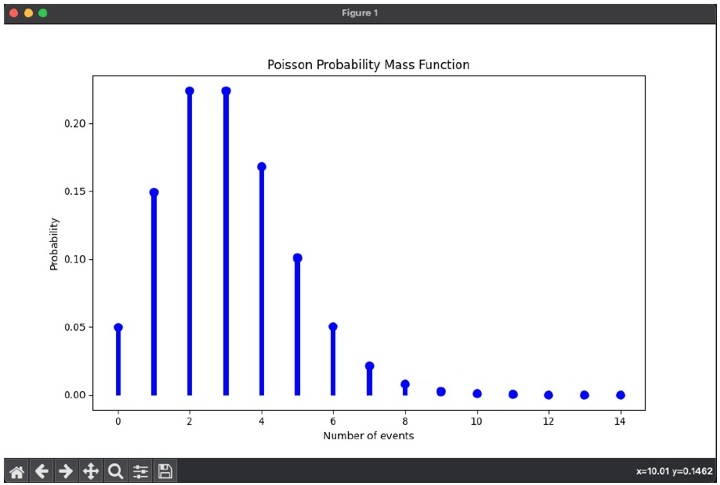
结论
总之,泊松概率质量函数 (PMF) 图是一种有用的可视化工具,可用于了解在时间或空间中随机发生的事件的概率分布。本文提供了两种在 Python 中创建泊松 PMF 图的方法。
第一种方法使用了 scipy 库,而第二种方法使用了 NumPy 和 Matplotlib 库。这两种方法都涉及定义泊松分布参数、计算概率质量函数以及使用适当的库绘制函数。方法的选择取决于用户对库的熟悉程度和特定的用例要求。

