在 Python 中实现雅可比法求解线性方程组
这是解决下面显示的线性方程组最直接的迭代策略。
$$\mathrm{a_{1,1}\: x_{1} \: + \: a_{1,2} \: x_{2} \: + \: \dotso\dotso \: + \: a_{1,n} \: x_{n} \: = \: b_{1}}$$
$$\mathrm{a_{2,1} \: x_{1} \: + \: a_{2,2} \: x_{2} \: + \: \dotso\dotso \: + \: a_{2,n} \: x_{n} \: = \: b_{2}}$$
$$\mathrm{\vdots}$$
$$\mathrm{a_{n,1} \: x_{1} \: + \: a_{n,2} \: x_{2} \: + \: \dotso\dotso \: + \: a_{n,n} \: x_{n} \: = \: b_{n}}$$
基本概念是:每个线性方程都重新组织通过将新变量移到左侧。然后从每个变量的初始猜测开始确定新值。在接下来的迭代中,新值将用作有根据的猜测。直到满足每个变量的收敛条件,重复此迭代过程,直到获得最终收敛答案。
雅可比算法
雅可比算法如下 -
从未知数 (x) 的一些初始猜测数组开始。
通过在重新排列的方程式中用 x 的猜测值替换 x 来评估新的 x,如下所示 -
$$\mathrm{x_{i_{new}} \: = \: − \frac{1}{a_{i,i}}(\sum_{j=1,j \neq i}^n a_{i,j}x_{j_{guess}} \: − \: b_{i})}$$
现在 $\mathrm{x_{i_{new}}}$ 将是从当前迭代中获得的新 x 值。
下一步是评估新值和猜测值之间的误差,即 $\mathrm{\lvert x_{new} \: − \: x_{guess} \rvert}$。如果误差超过某个收敛标准(我们将其设为 $\mathrm{10^{−5}}$),则将新值分配给旧猜测,即 $\mathrm{x_{guess} \: = \: x_{new}}$,然后开始下一次迭代。
否则,$\mathrm{x_{new}}$ 是最终答案。
Jacobi 算法 - 一个例子
让我们借助以下示例演示该算法 -
$$\mathrm{20x \: + \: y \: − \: 2z \: = \: 17}$$
$$\mathrm{3x \: + \: 20y \: − \: z \: = \: −18}$$
$$\mathrm{2x \: − \: 3y \: + \: 20z \: = \: 25}$$
将上述方程重新排列如下 −
$$\mathrm{x_{new} \: = \: (−y_{guess} \: + \: 2z_{guess} \: + \: 17)/20}$$
$$\mathrm{y_{new} \: = \: (−3x_{guess} \: + \: z_{guess} \: − \: 18)/20}$$
$$\mathrm{z_{new} \: = \: (−2x_{guess} \: + \: 3y_{guess} \: + \: 25)/20}$$
现在将在 while 循环中求解这些方程,以根据猜测值获得未知数的新值。
实现雅可比方法的 Python 程序
实现雅可比方法的程序(方程明智的实现)如下所示 -
示例
# 导入绘图和数组模块
来自 pylab 导入 *
来自 numpy 导入 *
# 初始猜测
xg=0
yg=0
zg=0
# 设置错误以进入 while 循环
error=1
# 设置迭代计数器
count=0
while error>1.E-5:
count+=1
#根据旧猜测评估新值
x=(17-yg+2*zg)/20
y=(zg-18-3*xg)/20
z=(25-2*xg+3*yg)/20
# 误差评估和绘图
error = abs(x-xg)+abs(y-yg)+abs(z-zg)
figure(1,dpi=300)
semilogy(count,error,'ko')
xlabel('iterations')
ylabel('error')
# 更新下一次迭代的猜测。
xg=x
yg=y
zg=z
savefig('error_jacobi.jpg')
print(f'x={round(x,5)}, y={round(y,5)}, z={round(z,5)}')
输出
程序输出将是
$$\mathrm{x \: = \: 1.0 \: , \: y \: = \: −1.0 \: , \: z \: = \: 1.0}$$
下图显示了每次迭代次数下误差的变化 −
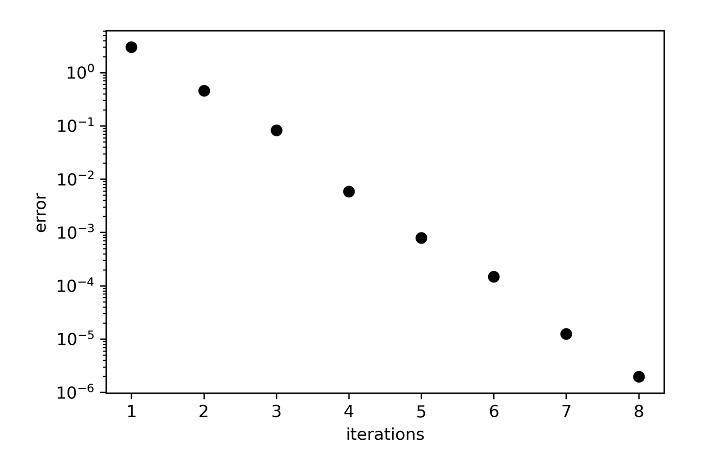
可以观察到,在第 8 次迭代时得到了收敛解。
但是,我认为如果我们可以将线性方程组的元素输入矩阵中,并以矩阵方式而不是方程形式求解它们,效果会更好。因此,执行此任务的程序代码如下 −
示例
# 导入模块
from pylab import *
from numpy import *
#-----------------------------------------#
# x 系数数组
a=array([[20,1,-2],[3,20,-1],[2,-3,20]])
# RHS 向量数组
b=array([17,-18,25])
# 行数和列数
n=len(b)
#-----------------------------------------#
# 设置初始猜测数组
xg=zeros(len(b))
# 启动错误以进入循环
error=1
# 设置迭代计数器
count=0
# 为新的 x 生成数组
xn=empty(len(b))
#-----------------------------------------#
while error>1.E-5:
count+=1
for i in range(n):
sum1=0
for j in range(n):
if i!=j:
sum1=sum1+a[i,j]*xg[j]
xn[i]=(-1/a[i,i])*(sum1-b[i])
# 误差评估和绘图
error = sum(abs(xn-xg))
figure(1,dpi=300)
semilogy(count,error,'ko')
xlabel('iterations')
ylabel('error')
# 将新值替换为下一次迭代的猜测值
xg=xn.copy()
#-----------------------------------------#
savefig('error_jacobi.jpg')
print('x: ',xn)
输出
x: [ 1.00000007 -0.99999983 1.00000005]

结论
在本教程中,我们解释了如何使用 Python 建模雅可比迭代法来解决联立线性方程。讨论了两种方法,即方程方法和矩阵方法。

