C++ 中二叉搜索树 II 中的中序后继
c++server side programmingprogramming更新于 2025/6/24 18:22:17
假设我们在二叉搜索树中有一个节点,我们需要在二叉搜索树中找到该节点的中序后继。如果没有中序后继,则返回 null。我们知道,一个节点的后继是键值小于该节点值的最小节点。
我们可以直接访问该节点,但不能访问树的根节点。这里每个节点都会有一个对其父节点的引用。以下是 Node − 的定义
class Node {
public int val;
public Node left;
public Node right;
public Node parent;
}
如果输入类似于 −
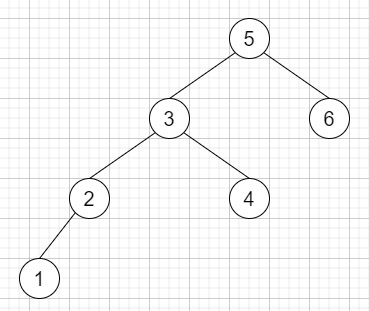
并且节点为 2,则输出为 3。
为了解决这个问题,我们将遵循以下步骤 −
如果节点右侧不为空,则 −
节点 := 节点右侧
如果节点左侧不为空,则执行 −
节点 := 左侧节点
返回节点
while (节点的父节点不为空且节点不等于节点父节点的左侧),执行 −
节点 := 节点的父节点
返回节点的父节点
示例
让我们看下面的实现,以便更好地理解 −
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int val;
Node* left;
Node* right;
Node* parent;
Node(int v, Node* par = NULL){
val = v;
left = NULL;
right = NULL;
parent = par;
}
};
class Solution {
public:
Node* inorderSuccessor(Node* node) {
if (node->right) {
node = node->right;
while (node->left)
node = node->left;
return node;
}
while (node->parent && node != node->parent->left) {
node = node->parent;
}
return node->parent;
}
};
main(){
Solution ob;
Node *root = new Node(5);
root->left = new Node(3, root);
root->right = new Node(6, root);
root->left->left = new Node(2, root->left);
root->left->right = new Node(4, root->left);
root->left->left->left = new Node(1, root->left->left);
cout << (ob.inorderSuccessor(root->left->left))->val;
}
输入
Node *root = new Node(5); root->left = new Node(3, root); root->right = new Node(6, root); root->left->left = new Node(2, root->left); root->left->right = new Node(4, root->left); root->left->left->left = new Node(1, root->left->left); (ob.inorderSuccessor(root->left->left))->val
输出
3

