在 Python 中为数值积分建模梯形规则
积分(定积分)的目的是计算两个极限 a 和 b 之间的函数曲线下的面积。下图将进一步阐明这一概念。
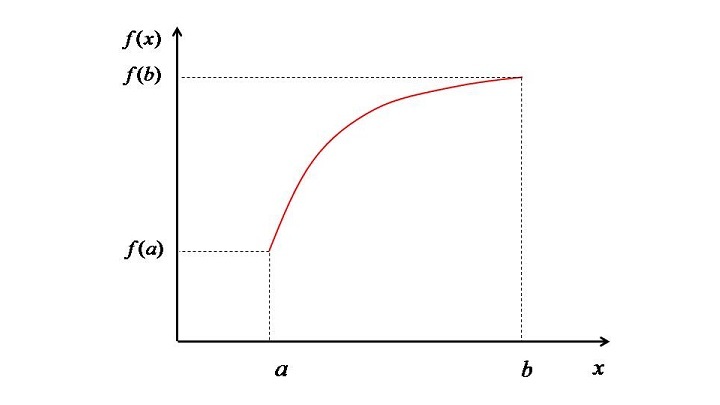
求积法,通常也称为数值积分,是一种用于评估给定函数曲线下面积的方法。该过程非常简单,即首先我们将有界区域划分为几个区域或条带。然后,借助简单矩形的数学公式来评估面积。然后将所有条带的面积相加,得到点 a 和点 b 之间函数曲线下的总面积。
在以下情况下,数值积分方法变得非常重要;
如果函数积分没有直接/明确的公式,或者,
积分必须在从经验数据中获得的某条曲线上进行。
数值积分方法的准确性取决于正确覆盖曲线下面积的条带/分区的数量。如果用最少的条带精确评估面积,则数值积分方法被称为最佳方法。
梯形法则
梯形法则是几十年来工程师用来执行数值积分任务的最基本技术。在这种方法中,给定曲线下的面积被划分为具有相同宽度 h 的垂直梯形,如下图所示。还可以观察到梯形的上部刚好接触曲线。
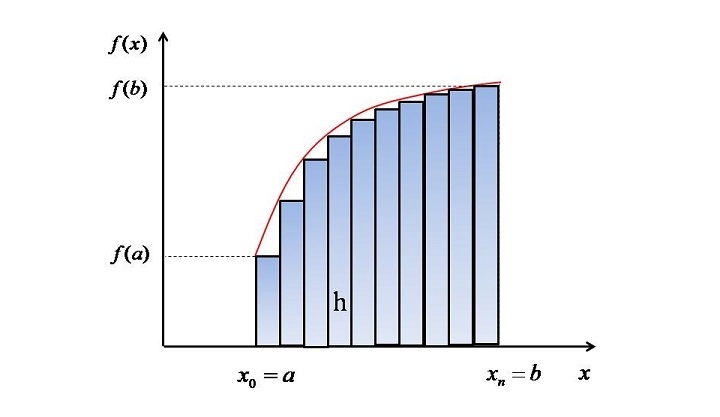
第一个梯形面积可以按以下方式计算 -
$$\mathrm{A_{1} \: = \: \frac{h}{2} \lgroup f(x_{0}) \: + \: f(x_{1}) \rgroup}$$
以类似的方式,可以评估其他矩形的连续面积。现在积分的基本原理是,每个梯形的面积必须从 $\mathrm{x_{0} \: = \: a}$ 添加到 $\mathrm{x_{n} \: = \: b}$ 才能得到积分 I。
从数学上讲,它可以写成 −
$$\mathrm{I \: = \: \frac{h}{2} \lgroup f(x_{0}) \: + \: f(x_{1}) \rgroup \: + \: \frac{h}{2} \lgroup f(x_{1}) \: + \: f(x_{2}) \rgroup \: + \: \: \dotso \: + \frac{h}{2} \lgroup f(x_{n-2}) \: + \: f(x_{n-1}) \rgroup \: + \frac{h}{2} \lgroup f(x_{n-1}) \: + \: f(x_{n}) \rgroup}$$
现在要注意的非常重要的一点是,从 $\mathrm{f(x_{1})}$ 到 $\mathrm{f(x_{n-1})}$ 函数出现了两次,所以除了第一项之外,它们都有系数 h $\mathrm{(f(x_{0}) \: = \: f(a))}$ 和最后一项 $\mathrm{(f(x_{1}) \: = \: f(b))}$。因此它们可以写成 −
$$\mathrm{I \: = \: h(\frac{1}{2} \lgroup f(a) \: + \: f(b) \rgroup \: + \: f(x_{1}) \: + \: f(x_{2}) \: + \: \: \dotso \: + \: f(x_{n-2}) \: + \: f(x_{n-1}) \rgroup}$$
在求和符号中(在任何编程语言中都非常容易实现和建模),上述等式也可以写成 −
$$\mathrm{I \: = \: h(\frac{1}{2} \lgroup f(a) \: + \: f(b) \rgroup \: + \: \sum_{i=1}^{i=n-1} f(x_{i}) )}$$
梯形规则在 Python 中的实现
要了解梯形规则在 Python 中的实现,让我们来解决以下问题 -
$$\mathrm{\int_{0}^{\frac{\pi}{2}} x \cos(x) \:dx}$$
现在该过程可以写成 -
导入模块
# 导入数组模块 from numpy import *
定义要执行积分的函数
# 定义函数 def f(x): return x*cos(x)
输入函数的左、右极限 (a, b) 以及要划分面积的梯形数量,即 n。
# 定义函数域(即左、右极限) a=0 b=pi/2 # 定义梯形数量 n=5
计算每个梯形的宽度 (h = (b − a)/n)
# 计算梯形的宽度 h=(b-a)/n
创建 x 数组。由于梯形的数量为 n,因此 x 的数量将为 n+1,即 x 数组将具有 n+1 个元素。这是因为 NumPy 数组的索引从 0 开始,而不是从 1 开始。
# 创建 x 数组 #(注意:对于 n 个梯形(x 的数量/节点 = n+1)) x=linspace(a,b,n+1)
首先评估 $\mathrm{\frac{1}{2} \lgroup f(a) \: + \: f(b) \rgroup}$ 并将结果分配给变量 I。
# 的第一项I I=0.5*(f(a)+f(b))
运行一个循环,对 x = 1 到 x = n 的 $\mathrm{\sum f(x_{i})}$ 进行求值(因为有 n + 1 个节点)。然后用 $\mathrm{I \: + \: \sum f(x_{i})}$ 更新 I 的值。最后在循环外将 I 乘以 h 并将其赋给 I。
# 对剩余的 n-2 个梯形求和 for j in range(1,n): I=I+f(x[j]) I=h*I
示例
完整程序如下 −
# 导入数组模块
from numpy import *
# 定义函数
def f(x):
return x*cos(x)
# 定义函数域(即左和右极限)
a=0
b=pi/2
# 定义梯形数量
n=5
# 评估梯形宽度
h=(b-a)/n
# 创建 x 数组
#(注意:对于 n 个梯形(x 的数量/节点 = n+1))
x=linspace(a,b,n+1)
# I 的第一项
I=0.5*(f(a)+f(b))
# 对剩余的 n-2 个梯形求和
for j in range(1,n):
I=I+f(x[j])
I=h*I
print(f'I = {round(I,6)}')
输出
上述程序的输出将是 −
I = 0.54959
如果要进一步提高结果的准确性,则必须增加梯形的数量。
如果我们对 n=10 运行上述代码,则程序输出将是 −
I = 0.570585
此结果精确到小数点后 5 位。
如果要应用上述程序,则必须更改上述函数、其极限 (a,b) 和梯形数量 (n)代码。
结论
在本教程中,使用 Python 演示了梯形法进行数值积分求值。我们详细解释了该方法和 Python 代码。

