使用 Python 建模二维热传导问题
在本教程中,我们将了解如何使用 Python 建模二维热传导方程。二维稳态、有热量产生的热传导方程可以用笛卡尔坐标表示如下 −
$$\mathrm{\triangledown^{2} T \: + \: \frac{q_{g}}{k} \: = \: \frac{\partial^{2}T}{\partial x^{2}} \: + \: \frac{\partial^{2}T}{\partial y^{2}} \: + \: \frac{q_{g}}{k} \: = \: 0 \:\:\dotso\dotso (1)}$$
这必须离散化为获得有限差分方程。让我们考虑如下所示的矩形网格。
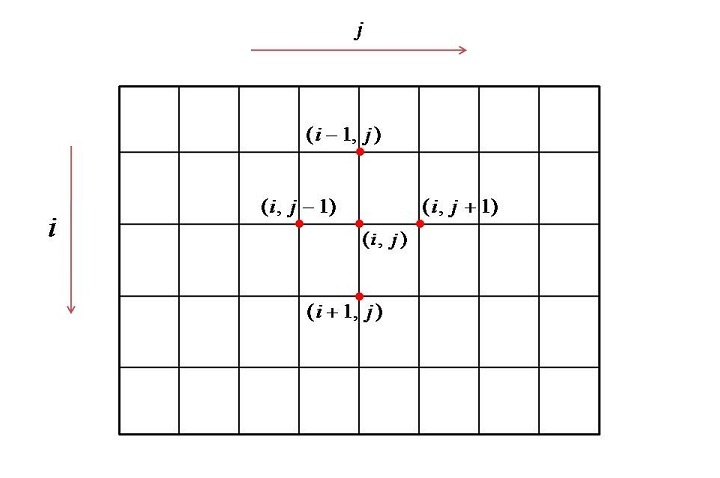
索引 𝑖 垂直运行,即按行运行,而索引 𝑗 水平运行,即按列运行。任何内部节点 (i,j) 都被四个节点包围,因此此节点处的信息只能从这四个节点传输。而对于边界节点,信息将来自边界条件。
为了离散化方程 1,将使用二阶精确的中心差分方案。而且,水平方向和垂直方向上的网格点之间的间距保持不变,即$\mathrm{\Delta x \: = \: \Delta y \: = \: \Delta}$。单变量函数二阶导数的中心差分公式为 −
$$\mathrm{\frac{d^{2}f(x)}{dx^{2}} \: = \: \frac{f_{i-1} \: − \: 2f_{i} \: + \: f_{i+1}}{\Delta x^{2}}\:\:\dotso\dotso (2)}$$
同样,Eq. 1 可以写成 −
$$\mathrm{\frac{T_{i-1, \: j} \: − \: 2T_{i,\: j} \: + \: T_{i+1, \: j}}{\Delta x^{2}} \: + \: \frac{T_{i, \: j-1} \: − \: 2T_{i,\: j} \: + \: T_{i, \: j+1}}{\Delta 6^{2}} \: + \: \frac{q_{g}}{k} \: = \: 0 \:\:\dotso\dotso (3)}$$
该方程的简化形式。 3 将是 −
$$\mathrm{T_{i,\: j} \: = \: \frac{1}{4}(T_{i-1, \: j}\: + \: T_{i+1, \: j} \: + \: T_{i,\: j-1} \: + \: T_{i, \: j+1} \: + \: \Delta^{2} \frac{q_{g}}{k}) \:\:\dotso\dotso (4)}$$
方程 4 是必须为方程中的每个内部节点求解的方程域。
对于这种类型的问题,信息从边界传递到内部,因此边界条件的知识至关重要。基本上,任何数值和分析分析中通常使用三种类型的边界条件,它们是-
狄利克雷:在这种情况下,因变量的值在边界处已知。例如
$$\mathrm{x \: = \: 0 \: \rightarrow \: T \: = \: 500 \: K }$$
纽曼:在这种情况下,因变量的导数给出为零或独立变量的函数。例如
$$\mathrm{x \: = \: 0 \: \rightarrow \: \frac{\partial T}{\partial x} \: = \: 0 }$$
Robin:在此,因变量的导数是因变量本身的某个函数。例如
$$\mathrm{− \: k \: (\frac{\partial T}{\partial x})_{x=0} \: = \: h(T \: − \: T_{\infty}) }$$
算法
选择域
选择 x 和 y 方向上的网格点数
定义 $\mathrm{\Delta x}$ 和 $\mathrm{\Delta y}$。
定义网格。
提供温度的初始猜测。
提供边界条件
求解方程 4 以获得内部节点
评估误差。
如果误差大于收敛标准,则将 T 的当前值设置为新的猜测并按照步骤 4-9 进行操作。否则,得出答案并绘制结果。
在本教程中,我们将解决两种情况,即有热量产生和没有热量产生。此外,我们将假设狄利克雷边界条件。
要解决的问题如下 −
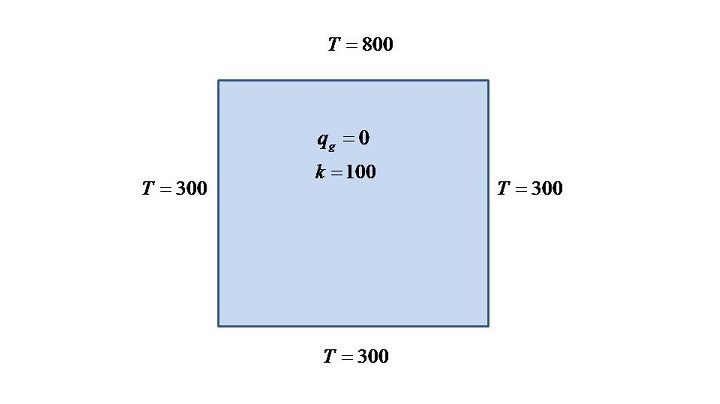
问题 1
问题 2
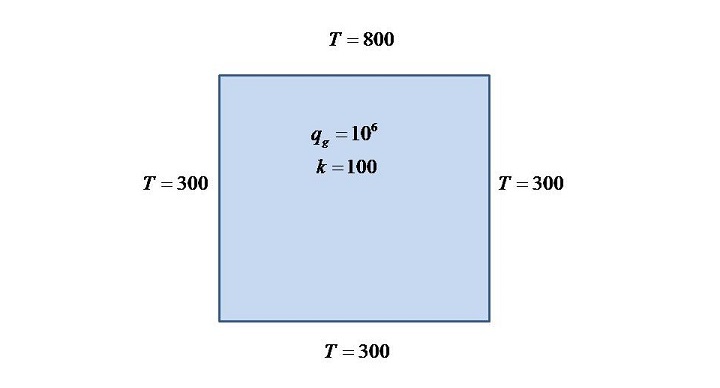
对于这两个问题,除了参数之外,其他一切都保持不变;热量产生。这就是为什么本文只显示一次代码的原因。
Importing modules
from pylab import *
from numpy import*
# 定义热特性
# 案例 1
# qg=0
# 案例 2
qg= 1000000
k=100
# 定义域
ℓx=1.0
ℓy=1.0
# 网格点数
nx=20
ny=20
# 网格间距
Δx=ℓx/(nx-1)
Δy=ℓy/(ny-1)
Δ=Δx
# 网格生成
x=linspace(0,ℓx,nx)
y=linspace(0,ℓy,ny)
X,Y=meshgrid(x,flipud(y))
# 初始猜测
T=zeros(shape=(nx,ny))
# 边界条件
#left
T[:,0]=300
#right
T[:,-1]=300
#top
T[0,:]=800
#bottom
T[-1,:]=300
# 猜测数组进行比较
Tg=T.copy()
# 初始错误或循环中的条目
error=1
# 迭代计数器
count=1
# 比较循环
while error>1.E-5:
# 在域内扫描
for i in range(1,nx-1):
for j in range(1,ny-1):
T[i,j]=(T[i,j-1]+T[i,j+1]+T[i-1,j]+T[i+1,j]+Δ**2*qg/k)/4
# 评估并打印错误
error=sqrt(sum(abs(T-Tg)**2))
figure(1,dpi=300)
if count%100==0:
print(error)
semilogy(count,error,'ko')
xlabel("Iteration Counter")
ylabel("Error")
savefig("Error.jpg")
# 更新下一次迭代的猜测
Tg=T.copy()
# 增加计数器
count+=
# 结果绘图(温度轮廓图)
figure(3,dpi=300)
cp1=contourf(X,Y,T,10,cmap='jet')
colorbar()
cp1=contour(X,Y,T,10,colors='k')
clabel(cp1,inline=True, fontsize=10)
savefig("temp.jpg")
第一种情况的误差和温度图
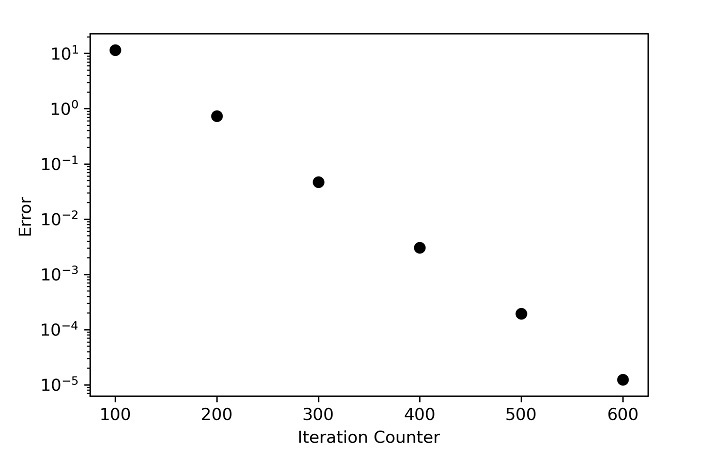
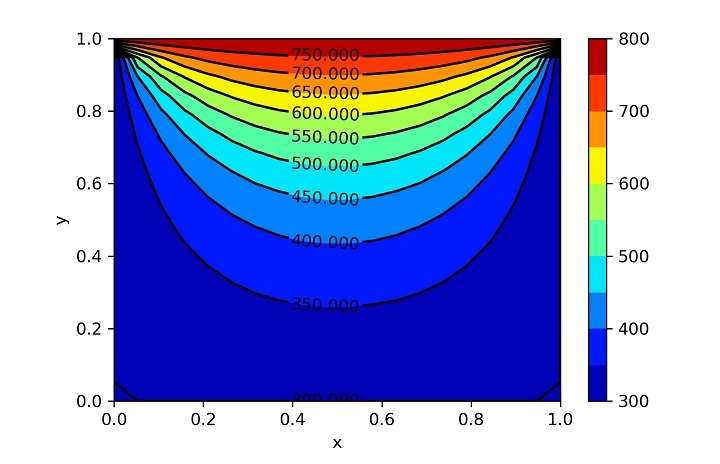
第二种情况的误差和温度图
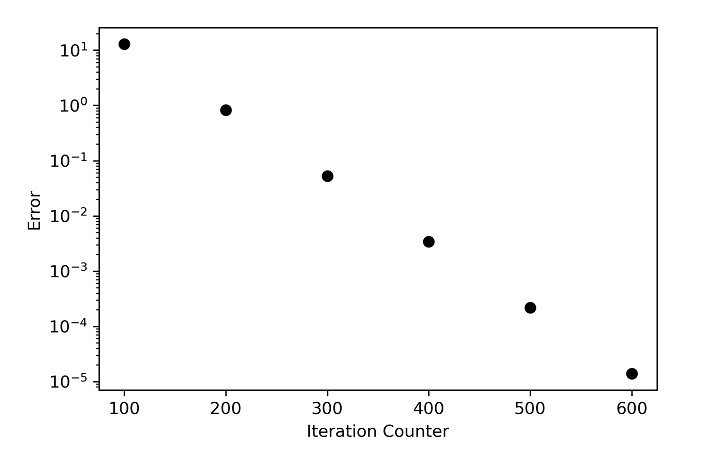

现在您可以观察到,热量产生的影响导致核心温度大幅升高,以至于边界条件的影响无法与之匹敌。在问题一中,您已经观察到影响从顶部开始,然后向下和侧面移动。然而,在第二种情况下,边界条件试图产生影响,但由于高热量产生,热流命令现在从中心开始并向外移动。尽管如此,由于问题必须与边界条件相匹配,边界温度保持不变。
结论
在本教程中,已使用 Python 建模了 2D 热传导方程。有限差分法已被用于解决两个问题:一个有热生成,一个没有热生成。据观察,代码中考虑的热量生成量对最终稳态解的影响不大。

