使用 Python 编写程序,查找具有最大概率的路径
pythonserver side programmingprogramming
假设我们有一个具有 n 个节点的无向加权图(节点从 0 开始编号),该图使用边列表作为输入,对于每个边 e,它具有成功遍历该边的概率 probability[e]。我们还有起始节点和终止节点,我们必须找到从起始到终止成功概率最大的路径并返回其成功概率。如果我们找不到任何路径,则返回 0。
因此,如果输入如下
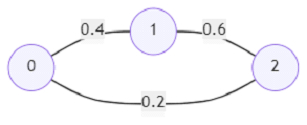
则输出将为 0.24,因为从节点 0 到 2 有两条路径,一条路径的概率为 0.2,另一条路径通过节点 1 的概率为 0.4*0.6 = 0.24,这是最大值。
为了解决这个问题,我们将遵循以下步骤 −
g := 根据给定的边列表制作图表并使用概率值作为权重
q := 队列数据结构
将 (start, 1) 插入 q
visited := 一个用于保存已访问节点的映射
当 q 不为空时,执行
(node, prob) := q 的第一个项目并将其从 q 中删除
如果 accessed[node] > prob,然后
进行下一次迭代
否则,
visited[node] := prob
对于 g[node] 中的每个相邻节点 adj 和概率 nextProb,执行
如果 visit[adj] < prob * nextProb,然后
在 q 末尾插入 (adj, prob * nextProb)
返回 visited[end]
让我们看看下面的实现以便更好地理解 −
示例
from collections import defaultdict, deque def solve(edges, probability, start, end): g = defaultdict(list) for i in range(len(edges)): src, dst = edges[i][0], edges[i][1] prob = probability[i] g[src].append((dst, prob)) g[dst].append((src, prob)) q = deque() q.append((start, 1)) visited = defaultdict(int) while q: node, prob = q.popleft() if visited[node] > prob: continue else: visited[node] = prob for adj, nextProb in g[node]: if visited[adj] < prob * nextProb: q.append((adj, prob * nextProb)) return visited[end] edges = [[0,1],[1,2],[0,2]] probability = [0.5,0.5,0.2] start = 0 end = 2 print(solve(edges, probability, start, end))
输入
[[0,1],[1,2],[0,2]], [0.5,0.5,0.2], 0, 2
输出
0.25


