复数的 Python 程序

pythonserver side programmingprogramming

正数总是有两个实根。例如，如果 x2 为 25，则 x 为 ±5。但是，如果 x2 为 -25，则不存在实根。任何负数的平方根都是其绝对值的平方根乘以虚数单位 j = √−1。

因此 √−25 = √25 𝑋−1 = √25 × √−1 = 5j

复数由实部和虚部组成。它表示为 x+yj。x 和 y 都是实数。 Y 乘以虚数单位形成复数的虚部。

示例:3+2j、10-5.5J、9.55+2.3j、5.11e-6+4j

Python 具有内置的复数数据类型。可以通过文字表示创建复数对象，如下所示 −

>>> x = 2+3j
>>> type(x)

复数对象有两个属性 real(返回实部)和 imag(返回不包括虚数单位 j 的虚部)

>>> x.real
2.0
>>> x.imag
3.0

它还具有 curriculum() 方法。复数的共轭具有相同的实部和虚部，但符号相反。因此，2+3j 的共轭是 2-3j

>>> x.curriculum()
(2-3j)

Python 还具有内置的 complex() 函数，该函数返回复数对象。该函数接受两个参数，一个用于实部，一个用于虚部。它们可以是任何数字类型(int、float 或 complex)

>>> complex(9,5)
(9+5j)
>>> complex(-6, -2.5)
(-6-2.5j)
>>> complex(1.5j, 2.5j)
(-2.5+1.5j)

如果只给出一个参数，则将其视为实部，虚部假定为零。

>>> complex(15)
(15+0j)

该函数还可以将字符串作为参数，前提是它包含数字表示。

>>> complex('51')
(51+0j)
>>> complex('1.5')
(1.5+0j)

复数的加减运算与整数或浮点数的加减运算类似。实部和虚部分别加/减。

>>> a = 6+4j
>>> b = 3+6j
>>> a+b
(9+10j)
>>> a-b
(3-2j)

对于乘法，将复数视为二项式，并将第一个数字中的每个项乘以第二个数字中的每个项。

a = 6+4j
b = 3+2j
c = a*b
c = (6+4j)*(3+2j)
c = (18+12j+12j+8*-1)
c = 10+24j

在 Python 控制台中，结果验证了这一点 −

>>> a = 6+4j
>>> b = 3+2j
>>> a*b
(10+24j)

复数的除法如下 −

设两个数为

a = 2+4j

b = 1-2j

我们想计算 a/b。

求分母的共轭，即 1+2j

将分子和分母乘以分母的共轭，得到除法结果

c = a/b
c = (2+4j)*(1+2j)/(1-2j)(1+2j)
c = (2+4j+4j+8*-1)/(1+2j-2j-4*-1)
c = (-6+8j)/5
c = -1.2+1.6j

以下 Python 控制台会话验证了上述处理。

>>> a = 2+4j
>>> b = 1-2j
>>> a/b
(-1.2+1.6j)

cmath 模块

Python 标准库 math 模块中定义的数学函数处理浮点数。对于复数，Python 库包含 cmath 模块。

复数 z = x+yj 是笛卡尔表示。它在内部以极坐标表示，其模数为 r(由内置 abs() 函数返回)和相位角 Φ(发音为 phi)，该角是 x 轴与 x 和原点连线之间的逆时针角度(以弧度为单位)。下图说明了复数的极坐标表示 −

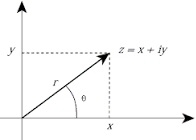
cmath 模块中的函数允许将笛卡尔表示转换为极坐标表示，反之亦然。

polar() − 此函数返回复数笛卡尔符号的极坐标表示。返回值是由模数和相位组成的元组。

>>> import cmath
>>> a = 2+4j
>>> cmath.polar(a)
(4.47213595499958, 1.1071487177940904)

请注意，模数由 abs() 函数返回

>>> abs(a)
4.47213595499958

phase() − 此函数返回 x 轴与连接 a 和原点的线段之间的逆时针角度。该角度以弧度表示，介于 π 和 -π 之间。

>>> cmath.phase(a)
1.1071487177940904
z = x+yj
Φ

rect() − 此函数返回以极坐标形式(即模数和相位)表示的复数的笛卡尔表示形式。

>>> cmath.rect(4.47213595499958, 1.1071487177940904)
(2.00000000000000004+4j)

cmath 模块包含 math 模块中定义的所有数学函数的替代方案。有三角函数和对数函数，如下所述 −

cmath.sin() − 此函数返回以弧度表示的相位角的正弦三角比。

>>> import cmath
>>> a = 2+4j
>>> p = cmath.phase(a)
>>> cmath.sin(p)
(0.8944271909999159+0j)

类似地，cmath 模块中定义了其他比率函数 cos()、tan()、asin()、acos() 和 atan()。

cmath.exp() − 与 math.exp() 类似，此函数返回 ex，其中 x 是复数，e 为 2.71828

>>> cmath.exp(a)
(-1.1312043837568135+2.4717266720048188j)

cmath.log10() − 此函数计算以 10 为底的复数的对数值

>>> a = 1+2j
>>> cmath.log10(a)
(0.3494850021680094+0.480828578784234j)

cmath.sqrt() − 此函数返回复数的平方根。

>>> cmath.sqrt(a)
(1.272019649514069+0.7861513777574233j)

在本文中，我们了解了 Python 复数数据类型的重要特性以及如何对其进行算术运算。我们还探索了 cmath 模块中定义的各种函数。