在标记邻居的最短路径后查找图中所有剩余顶点

与图搜索算法有关的算法遍历图以进行广泛发现或有针对性的搜索。这些算法在网络中切割路径，但没有人期望这些路径在计算上是最优的。寻路算法是基于图搜索技术组装的，这些算法研究顶点之间的路径，从特定节点开始并通过连接直到访问目标。

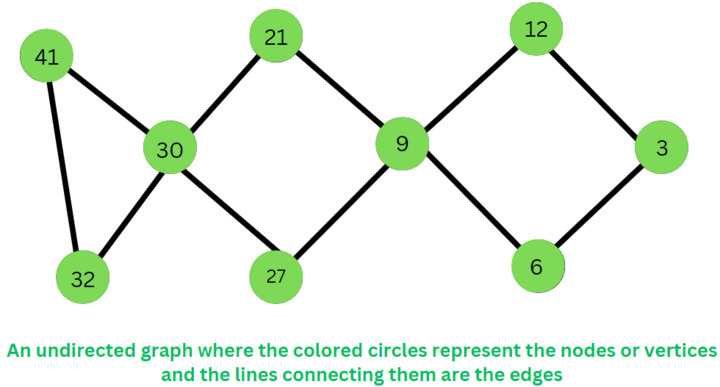
什么是图？

图是反映组件集之间"连接"的数据结构。

这些项目称为节点。边是节点之间的连接。

最短路径

最短路径算法定位任意两个节点或顶点之间的最短路径或权重最小的边。由于它是实时运行的，因此非常适合用户交互和动态工作流程。

Dijkstra 算法

Dijkstra 算法构造一组与源距离最小的节点，以便仅从一个源节点获得"最短路径树"。

Dijkstra 算法的基本原理是什么？

Dijkstra 算法的基本原理如下 -

• Dijkstra 算法从您指定的节点（也称为起始节点）开始，然后继续分析图形以发现连接该顶点和图形内所有其他节点的最短路径。

• 此技术跟踪源节点和每个节点之间的最短距离，并在识别或检测到更短路线时更改值。

• 一旦找到连接源和其他节点的最小距离，该顶点将被标记为"访问过"并添加到路径中。

• 重复该技术，直到图中的所有顶点都包含在路径中。因此，人们建立了通过到每个节点的最短可行路径将主节点链接到每个节点的路径。

注意

图形分析在描述链接和路径时将使用术语，例如 -

• "权重" - 关系特定特征的数字实体。

• "成本" - 在评估路径的总体权重时我们会经常遇到它。

• "距离"是连接属性的常用名称，它反映了算法中跨两个节点的行进距离。

• "跳跃"是指跨两个顶点的连接数。

Dijkstra 算法的主要用途

该方法确定 GPS 设备中连接当前位置和目标位置的最短路线。它在工业中有多种用途，主要是在需要网络建模的领域。

如果图的边具有负权重，Dijkstra 算法还能工作吗？

答案是否定的。

Dijkstra 算法只能在具有正权重的图中起作用。这是因为必须添加边的权重才能检测出最短路线。

对于具有负权重的图，该算法无法成功运行。当节点被标记为"已访问"时，通向该节点的当前路径将成为最短路径。负权重可以改变这一点，因为这个阶段之后总权重会减少。

在完成标记图中邻居的最短路径以识别所有剩余顶点后，该做什么？

该过程是遍历每个顶点并标记具有最小列号的节点，该节点通过最小权重边链接到主顶点。通过最小权重边链接到当前节点的顶点，然后发现每个未标记的边。

要解决这个问题，请按照以下步骤操作

使用两个循环 j 和 i 遍历整个邻接矩阵。

确定邻接矩阵中每个（行）的最小结果；列号最小的节点通过权重最小的边链接到主顶点。

使用布尔数组，为每个顶点标记此顶点。

打印布尔数组中未标记的每个顶点或节点。

此方法的实现如下

示例

#include <iostream>
#include <string>
#include <vector>
#include <limits>
 
// Stdc++11 代码来实现该方法
class GFG{
   
   // 计算未标记边的数量的函数
   public:
   static std::vector<bool> markedNodesCounter(std::vector<std::vector<int>> &A, int V){
       
    // 初始化访问数组
    std::vector<bool> marked(V);
    
    // 循环遍历每个节点
    for (int i = 0; i < V; i++){

        // 初始化最小距离和与当前节点最近的节点
        int minweight = std::numeric_limits<int>::max();
        int min = V + 1;
        
        // 循环查找从当前节点到其他每个节点的权重
        for (int j = 0; j < V; j++){
            if (i == j){
               continue;
            }
            if (A[i][j] < minweight){
               minweight = A[i][j];
               min = j;
            }
         }
         // 标记最近节点
         marked[min] = true;
      }
      // 返回答案
      return marked;
   }
   // 驱动代码
   static void main(std::vector<std::string> &args){
      int V = 3;
      std::vector<std::vector<int>> A{{0, 10, 50}, {10, 0, 30}, {50, 30, 0}};
      // 获取结果
      std::vector<bool> marked = GFG::markedNodesCounter(A, V);
      // 打印结果
      bool flag = false;
      for (int i = 0; i < V; i++){
         if (!marked[i]){
            std::cout << std::to_string(i) + " ";
            flag = true;
         }
      }
      if (!flag){
         std::cout << "-1" << std::endl;
      }else{
         std::cout << std::endl;
      }
   }
};
int main(int argc, char **argv){
   std::vector<std::string> parameter(argv + 1, argv + argc);
   GFG::main(parameter);
   return 0;
};

输出

根据上述代码 −

2

辅助空间为 O(V)，时间复杂度为 O(V2)，用于生成一个大小为 V 的附加数组并初始化两个分别从 0 到 V 的嵌套循环。

什么情况需要最短路径？

使用最短路径算法，您可以根据跳数或任何其他加权连接值确定两个节点之间的最佳路径。它可以提供有关分离度、两个位置之间的最小路线或最便宜方式的即时响应。人们也可以利用这种方法来调查特定节点之间的关系。

结论

寻路算法可以帮助我们理解数据之间的关系。Dijkstra 算法发现网络中两个节点之间的最短路线。该方法采用边权重来检测减少连接主顶点和所有顶点的整个权重的路径。

相关文章

• 图中的团
• 无权图的应用、优点和缺点
• 在标记邻居的最短路径后查找图中所有剩余顶点
• 计算给定数字字符串连接 K 次后生成的字符串中 01 的子序列
• 查找字符串字母值的个位数和
• String 可以被视为关键字吗?
• 通过将辅音替换为最接近的元音或将辅音替换为最接近的元音来计算唯一字符串的数量
• 在给定的对中找出平均值刚好大于当前对的对的索引
• 斐波那契数列中每个元素的阶乘
• 斐波那契系数和斐波那契三角形