MATLAB 中的灰度共生矩阵
在数字图像处理中,灰度共生矩阵,也称为GLCM,是一种用于保存数字图像中像素对之间的空间关系的统计方法。
灰度共生是一种表示图像中不同像素强度组合排列方式的方法。它主要用于指定图像的纹理属性,并提供有关图像空间区域内像素值中出现的模式、变化和结构的信息。
什么是灰度共生矩阵?
如上所述,灰度共生矩阵 (GLCM) 是一种统计方法,可提供有关图像指定局部区域中像素强度之间关系的信息。
灰度共生矩阵基本上是一个方阵,其元素表示图像中像素出现的频率。这种技术在图像处理应用中获取图像中存在的纹理和图案信息时非常有用。
如何在 MATLAB 中计算灰度共生矩阵?
MATLAB 提供了一个内置函数"geaycomatrix"来计算图像中的灰度共生矩阵。
此函数可以有以下三种语法:
glcm = graycomatrix(I) glcm = graycomatrix(I, Name, Value) [glcm, SI] = graycomatrix(___)
我们将在本文的后续部分介绍所有这些语法。在此之前,让我们了解一下使用 MATLAB 计算灰度共生矩阵的分步过程。
计算灰度共生矩阵的过程
使用 MATLAB 从图像计算灰度共生矩阵的分步过程如下:
步骤 (1) – 读取输入图像并将其转换为灰度版本。
步骤 (2) – 定义用于计算灰度共生矩阵的参数,例如像素对之间的距离、角度等。
步骤 (3) – 使用"graycomatrix"函数计算灰度共生矩阵。
然后可以使用此灰度共生矩阵来分析图像的纹理和图案属性。
现在,让我们实际了解如何在 MATLAB 中从图像创建灰度共生矩阵。
使用默认参数计算灰度共生矩阵
在 MATLAB 中,我们可以使用"graycomatrix"函数的以下语法,使用默认参数从图像创建灰度共生矩阵 (GLCM)。
glcm = graycomatrix(I);
其中,I 是输入的灰度图像。
示例
现在让我们考虑一个示例程序来演示此语法在 MATLAB 编程中的实现。
% MATLAB 程序使用默认参数创建 GLCM
% 读取输入图像
img = imread('https://www.tutorialspoint.com/assets/questions/media/14304-1687425236.jpg');
% 将输入图像转换为灰度图像
I = rgb2gray(img);
% 使用默认参数计算 GLCM
glcm = graycomatrix(I);
% 显示 GLCM
disp('输入图像的 GLCM 是:');
disp(glcm);
输出
输入图像的 GLCM 为: 33 129 41 14 1 0 0 0 135 2874 778 223 84 24 3 0 31 791 22294 3199 329 125 35 1 15 174 3236 28009 3252 394 152 16 3 106 311 3128 14310 2148 317 74 1 42 140 485 1775 12637 2085 200 0 6 59 186 513 1594 24010 2485 0 0 6 40 155 484 2289 136872
使用指定参数计算灰度共生矩阵
在 MATLAB 中,使用以下语法的"graycomatrix"函数使用指定参数计算灰度共生矩阵。
glcm = graycomatrix(I, Name, Value, …);
在此语法中,我们使用名称-值对指定参数。
示例
以下示例演示了此语法在 MATLAB 编程中的实际实现。
% MATLAB 程序使用指定参数创建 GLCM
% 读取输入图像
img = imread('https://www.tutorialspoint.com/assets/questions/media/14304-1687425236.jpg');
% 将输入图像转换为灰度图像
I = rgb2gray(img);
% 使用默认参数计算 GLCM
glcm = graycomatrix(I, 'Offset', [2 1], 'NumLevels', 7);
% 显示 GLCM
disp('输入图像的 GLCM 为:');
disp(glcm);
输出
输入图像的 GLCM 为: 53 193 33 26 34 53 54 206 4087 1611 406 243 190 283 26 1607 32291 5636 1006 486 352 24 413 5511 20083 3230 844 604 29 236 1051 2957 11465 2442 768 49 201 555 808 1938 20689 3416 57 284 410 811 1073 2974 139777
计算灰度共生矩阵并返回缩放后的图像
在 MATLAB 中,以下"graycomatrix"函数的语法用于计算返回缩放后的图像的灰度共生矩阵。
[glcm, SI] = graycomatrix(___);
此处,变量"SI"是缩放后的图像,基本上是归一化到范围 [1, NumLevels] 的输入图像。
示例
让我们看一个例子来了解此语法在 MATLAB 编程中的实现。
% MATLAB 程序创建 GLCM 返回缩放后的图像
% 读取输入图像
img = imread('https://www.tutorialspoint.com/assets/questions/media/14304-1687425236.jpg');
% 将输入图像转换为灰度图像
I = rgb2gray(img);
% 使用默认参数计算 GLCM
[glcm, SI] = graycomatrix(I);
% 显示 GLCM 和缩放后的图像
disp('输入图像的 GLCM 为:');
disp(glcm);
disp('缩放后的图像为:');
imshow(rescale(SI));
输出
输入图像的 GLCM 为:
The GLCM for the input image is: 33 129 41 14 1 0 0 0 135 2874 778 223 84 24 3 0 31 791 22294 3199 329 125 35 1 15 174 3236 28009 3252 394 152 16 3 106 311 3128 14310 2148 317 74 1 42 140 485 1775 12637 2085 200 0 6 59 186 513 1594 24010 2485 0 0 6 40 155 484 2289 136872
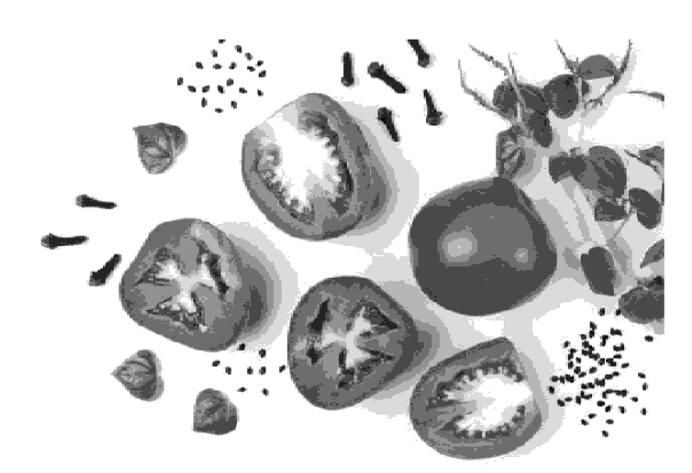
缩放后的图像为:
结论
这一切都是关于在 MATLAB 中创建灰度共生矩阵 (GLCM)。为此,MATLAB 提供了一个内置函数"graycomatrix",允许从图像中计算共生矩阵以分析图像的纹理特征。
在本教程中,我们解释了灰度共生矩阵的概念、它在图像处理中的重要性以及实际示例,以了解如何使用 MATLAB 计算图像的 GLCM。


