莱布尼茨调和三角形
莱布尼茨调和三角形,也称为莱布尼茨级数或莱布尼茨公式,是由德国数学家兼哲学家戈特弗里德·威廉·莱布尼茨于 17 世纪末发现的一种三角形数字排列。
莱布尼茨调和三角形是分数的三角形排列。我们从顶部的数字开始,最外层的项是表示该特定行号的自然数的倒数。一般来说,莱布尼茨谐波三角形中的项可以通过以下方程确定,其中 r 为行数,c 为列数,条件是 c <= r
L(r,c)=L(r-1,c-1) - L(r,c-1),其中 L(r,1)=1/r
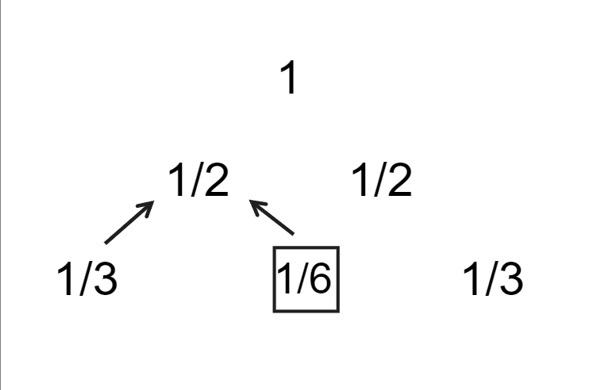
下图展示了莱布尼茨谐波三角形的前三行。
问题描述
给定一个数字 n,生成 n 行的莱布尼茨谐波三角形。
示例
输入
n = 3
输出
1/1 1/2 1/2 1/3 1/6 1/3
解释
当 n = 3 时,莱布尼茨谐波三角形有三行。每行最外层的项 = 1/(行号)。
为了生成此三角形,我们从第一行开始,即 1/1。然后,对于第二行,我们计算每个单元格的值,即左上角单元格的值减去左边单元格的值:
L(2, 1) = 1/2
L(2, 2) = 1/2
因此第二行是 1/2 1/2。
最后,对于第三行,我们再次计算每个单元格的值,即左上角单元格的值减去左边单元格的值。
L(3,1) = L(3,3) = 1/3
L(3,2) = L(2,1) - L(3,1) = 1/6
输入
n = 4
输出
1/1 1/2 1/2 1/3 1/6 1/3 1/4 1/12 1/12 1/4
解释
直到 n = 3,方法与上例相同。
对于第四行
L(4,1) = L(4,4) = 1/4
L(4,2) = L(3,1) - L(4,1) = 1/3 - 1/4 = 1/12
L(4,3) = L(3,2) - L(4,2) = 1/6 - 1/12 = 1/12
解决方案
伪代码
开始
将 n 的值初始化为 4。
声明一个具有 n+1 行和 n+1 列的二维向量 L,并初始化将所有元素设置为 0。
使用参数 n 和 L 调用函数 LHT。
在函数 LHT 中,从 i=0 迭代到 i<=n。
在上述循环中,从 j=0 迭代到 j<=min(i,n)。
在上述循环中,如果 j==0 或 j==i,则将 L[i][j] 的值设置为 1。
否则,将 L[i][j] 的值设置为 L[i-1][j-1]+L[i-1][j]。
使用参数 n 和 L 调用函数 printLHT。
在函数 printLHT 中,从 i=1 迭代到i<=n。
在上述循环中,从 j=1 迭代到 j<=i。
在上述循环中,打印"1/",然后打印 i*L[i-1][j-1]。
每次内循环完成后,打印一个新行。
结束。
算法
function LHT()
for i = 0 to n do
for j = 0 to min(i, n) do
if j == 0 or j == i then
L[i][j] = 1
else
L[i][j] = L[i-1][j-1] + L[i-1][j]
end if
end for
end for
printLHT(n, L)
end function
function printLHT()
for i = 1 to n do
for j = 1 to i do
print "1/" + i*L[i-1][j-1] + " "
end for
print new line
end for
end function
function main
Initialize n = 4
L = 2D vector of size n + 1 x n + 1, with all elements initialized to 0
LHT(n, L)
return 0
示例:C++ 程序
以下 C++ 程序使用函数 LHT() 和 printLHT() 生成并打印给定行数的莱布尼茨谐波三角形。main() 函数初始化行数,并创建一个大小为 n + 1 * n + 1 的二维向量"L"来存储项。
// 用于打印莱布尼茨谐波三角形的 CPP 程序
#include <bits/stdc++.h>
using namespace std;
// 用于打印莱布尼茨谐波三角形的函数
void printLHT(int n, vector<vector<int>> L){
for (int i = 1; i <= n; i++){
for (int j = 1; j <= i; j++)
cout << "1/" << i * L[i - 1][j - 1] << " ";
cout << endl;
}
}
// 生成莱布尼茨谐波三角形的函数
void LHT(int n, vector<vector<int>> &L){
for (int i = 0; i <= n; i++){
for (int j = 0; j <= min(i, n); j++){
if (j == 0 || j == i)
L[i][j] = 1;
// 使用先前存储的值生成值
else
L[i][j] = L[i - 1][j - 1] + L[i - 1][j];
}
}
// 打印莱布尼茨谐波三角形
printLHT(n,L);
}
// Main function
int main(){
int n = 5;
// 用于存储莱布尼茨谐波三角形的二维向量
vector<vector<int>> L(n + 1, vector<int>(n + 1, 0));
LHT(n, L);
return 0;
}
输出
1/1 1/2 1/2 1/3 1/6 1/3 1/4 1/12 1/12 1/4 1/5 1/20 1/30 1/20 1/5
时间和空间复杂度分析
时间复杂度:O(n2)
本程序的时间复杂度为 O(n2),其中 n 是莱布尼茨谐波三角形的行数。这是因为程序通过将每个元素计算为前两个元素之和来生成三角形,而三角形中有 n2 个元素。
空间复杂度:O(n2)
本程序的空间复杂度也是 O(n2),因为它将整个三角形存储在一个大小为 (n + 1) * (n + 1) 的二维向量中。
结论
在上文中,我们讨论了一种生成给定行数的莱布尼茨谐波三角形的方法。莱布尼茨谐波三角形是一个有趣的数学概念,类似于帕斯卡三角形。本文讨论了该概念、实现、求解方法以及伪代码、所用算法和 C++ 程序。我们还分析了该方案的时间和空间复杂度。

