使用 Python 建模斯特林和埃里克森循环
斯特林循环
斯特林循环由四个过程组成:两个可逆等容过程和两个可逆等温过程。在相同的温度范围内,理想再生斯特林循环的效率与卡诺循环相当。热相互作用贯穿整个循环,而功相互作用仅发生在过程 1-2 和 3-4 中。
下图显示了循环的示意图。
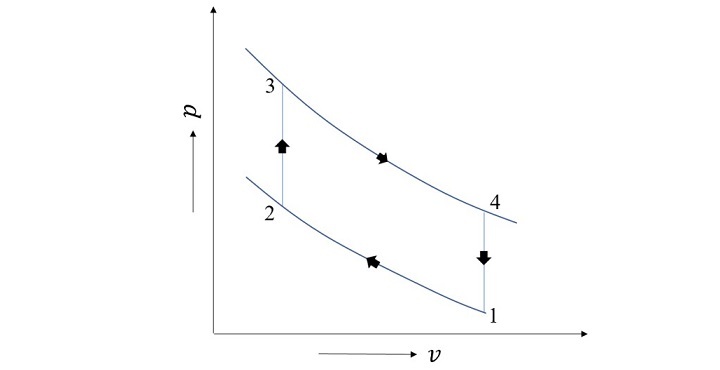
最大压力 $\mathrm{(p_{max})}$、最小压力 $\mathrm{(p_{min})}$、最大体积 $\mathrm{(v_{max})}$、压缩比 (r) 和绝热指数 $\mathrm{(\gamma)}$ 是循环建模时要考虑的输入变量。以下列表包括斯特林循环各个阶段涉及的几个过程的热力学计算 −
过程 1-2
$$\mathrm{p_{1} \: = \: p_{min}}$$
$$\mathrm{v_{1} \: = \: v_{max}}$$
首先,将根据点 1 处的体积使用压缩比 (r) 评估点 2 处的体积,如下所示 −
$$\mathrm{v_{2} \: = \: \frac{v_{1}}{r}}$$
然后,将过程 1-2 中的等温常数评估为−
$$\mathrm{c_{1} \: = \: p_{1} \: \times \: v_{1}}$$
点 2 处的压力可计算为 −
$$\mathrm{p_{2} \: = \: \frac{c_{1}}{v_{2}}}$$
一旦知道 $\mathrm{c_{1}}$,沿线 1-2 的压力变化可计算为 −
$$\mathrm{p \: = \: \frac{c_{1}}{v}}$$
过程2-3
$$\mathrm{p_{3} \: = \: p_{max}}$$
由于该过程是等容的,因此体积保持不变,因此 −
$$\mathrm{v_{3} \: = \: v_{2}}$$
因此,可以轻松评估 2 和 3 之间的压力变化。
过程 3-4
让 $\mathrm{c_{2}}$ 成为沿线 3-4 的常数。由于点 3 处的压力和温度已知,因此等温线上的常数可计算为 −
$$\mathrm{c_{2} \: = \: p_{3} \: \times \: v_{3}}$$
又由于 $\mathrm{v_{4} \: = \: v_{1}}$,因此点 4 处的压力可计算为 −
$$\mathrm{p_{4} \: = \: \frac{c_{2}}{v_{4}}}$$
因此,沿 3-4 处的压力变化可计算为 −
$$\mathrm{p \: = \: \frac{c_{2}}{v}}$$
过程 4-1
由于 $\mathrm{p_{1}}$ 和 $\mathrm{p_{4}}$ 已知,因此可以轻松评估 $\mathrm{v_{4} \: =}$ 恒定线的压力变化。
斯特林循环的 Python 程序
斯特林循环的 Python 函数如下 −
示例
from pylab import*
from pandas import*
#~~~~~~~~~~~~~~~~~~~~~
# Stirling Cycle
#~~~~~~~~~~~~~~~~~~~~~
def stirling(p_min,p_max,v_max,r,gma):
font = {'family' : 'Times New Roman','size' : 40}
figure(figsize=(20,15))
rc('font', **font)
'''This function prints Stirling cycle
arguments are as follows:
p_min: minimum pressure
p_max: Maximum pressure
v_max: Maximum volume
r: compression ratio
gma: Adiabatic exponent
The order of arguments is:
p_min,p_max,v_max,r,gma
'''
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 1-2
#~~~~~~~~~~~~~~~~~~~~~~~~~
p1=p_min
v1=v_max
c1=p1*v1
v2=v1/r
p2=c1/v2
v=linspace(v2,v1)
p=c1/v
plot(v,p/1000,'r',linewidth=2)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 2-3
#~~~~~~~~~~~~~~~~~~~~~~~~~
p3=p_max
v3=v2
v=zeros(100)+v3
p=linspace(p2,p3,100)
plot(v,p/1000,'b',linewidth=2)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 3-4
#~~~~~~~~~~~~~~~~~~~~~~~~~
c2=p3*v3
v4=v1
p4=c2/v4
v=linspace(v3,v4,100)
p=c2/v
plot(v,p/1000,'g',linewidth=2)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 4-1
#~~~~~~~~~~~~~~~~~~~~~~~~~
p=linspace(p1,p4,100)
v=zeros(100)+v1
plot(v,p/1000,'m',linewidth=2)
title('Stirling Cycle',size='xx-large',color='k')
xlabel('Volume (m$^3$)')
ylabel('Pressure (kPa)')
#axis([0.01,v4+0.01,p_min/1000-100,p_max/1000+100])
#grid(linestyle='--',color='k')
text(v1,p1/1000-80,'1')
text(v2-0.01,p2/1000,'2')
text(v3-0.01,p3/1000-20,'3')
text(v4,p4/1000+30,'4')
data={'p':[p1,p2,p3,p4],
'v':[v1,v2,v3,v4],
'c':[c1,'' ,c2,"" ],
'State': [1,2,3,4]}
df=DataFrame(data)
savefig('stirling_final.jpg')
return df.set_index('State')
sc=stirling(10**5,20*10**5,0.5,5,1.4)
show()
输出
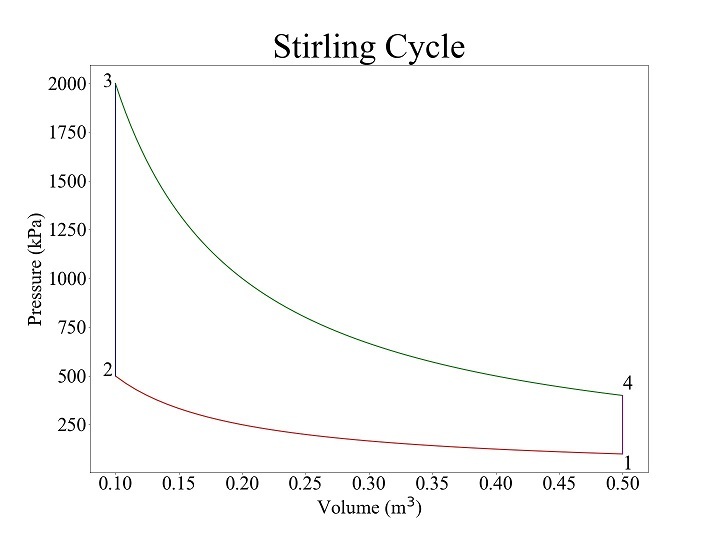
对于 $\mathrm{p_{min} \: = \: 10^{5} \: Pa \:, \: p_{max} \: = \: 20 \: \times \: 10^{5} \: Pa \:, \: v_{max} \: = \: 0.5 \: m^{3} \:, \: r \: = \: 5 \: and \: y \: = \: 1.4}$,程序结果如下 −
爱立信循环
爱立信循环由两个可逆等压过程和两个可逆等温过程组成。在相同的温度范围内,理想的再生爱立信循环与卡诺循环一样高效。此循环中的所有过程都与热量和功相互作用。下图描绘了该循环的示意图。

最大压力 $\mathrm{(p_{max})}$、最小压力 $\mathrm{(p_{min})}$、最大体积 $\mathrm{(v_{max})}$、恒压散热期间的压缩比 (r) 和绝热指数 $\mathrm{(\gamma)}$ 是循环建模时要考虑的输入变量。爱立信循环中各个过程的热力学计算如下所述 -
过程 1-2
$$\mathrm{p_{1} \: = \: p_{min}}$$
$$\mathrm{p_{2} \: = \: p_{1}}$$
$$\mathrm{v_{1} \: = \: v_{max}}$$
首先,将根据点 1 处的体积,使用压缩比 (r) 评估点 2 处的体积 -
$$\mathrm{v_{2} \: = \: \frac{v_{1}}{r}}$$
由于1-2 是等压过程,并且已知极端体积,因此可以轻松评估压力变化。
过程 2-3
沿等温线 2-3 的常数 $\mathrm{c_{1}}$ 可以计算为 −
$$\mathrm{c_{1} \: = \: p_{2} \: \times \: v_{2}}$$
由于 $\mathrm{p_{3} \: = \: p_{max}}$,因此点 3 处的体积可以计算为 −
$$\mathrm{v_{3} \: = \: \frac{c_{1}}{p_{3}}}$$
压力变化可以计算为 −
$$\mathrm{p \: = \: \frac{c_{1}}{v}}$$
过程 3-4
$$\mathrm{p_{4} \: = \: p_{3}}$$
让 $\mathrm{c_{2}}$ 成为线 4-1 上的常数。由于点 1 处的压力和体积已知,因此等温线 4-1 上的常数可以计算为 −
$$\mathrm{c_{2} \: = \: p_{1} \: \times \: v_{1}}$$
因此,点 4 处的体积可以计算为 −
$$\mathrm{v_{4} \: = \: \frac{c_{2}}{p_{4}}}$$
由于最终体积已知,因此可以轻松计算压力变化。
过程 4-1
由于 $\mathrm{v_{1}}$ 和 $\mathrm{v_{4}}$ 以及常数已知$\mathrm{c_{2}}$ 因此压力变化可以计算为 −
$$\mathrm{p \: = \: \frac{c_{2}}{v}}$$
爱立信循环的 Python 程序
用于模拟爱立信循环的 Python 函数如下 −
示例
from pylab import*
from pandas import*
#~~~~~~~~~~~~~~~~~~~~~
# Ericsson Cycle
#~~~~~~~~~~~~~~~~~~~~~
def ericsson(p_min,p_max,v_max,r,gma):
font = {'family' : 'Times New Roman','size' : 39}
figure(figsize=(20,15))
rc('font', **font)
'''This function prints Ericsson cycle
arguments are as follows:
p_min: minimum pressure
p_max: Maximum pressure
v_max: Maximum volume
r: compression ratio
gma: Adiabatic exponent
The order of arguments is:
p_min,p_max,v_max,r,gma
'''
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 1-2
#~~~~~~~~~~~~~~~~~~~~~~~~~
p1=p_min
p2=p1
v1=v_max
v2=v1/r
p=zeros(100)+p2
v=linspace(v2,v1,100)
plot(v,p/1000,'r',linewidth=2)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 2-3
#~~~~~~~~~~~~~~~~~~~~~~~~~
c1=p2*v2
p3=p_max
v3=c1/p3
v=linspace(v3,v2,100)
p=c1/v
plot(v,p/1000,'b',linewidth=2)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 3-4
#~~~~~~~~~~~~~~~~~~~~~~~~~
p4=p3
c2=p1*v1
v4=c2/p4
p=zeros(100)+p4
v=linspace(v3,v4,100)
plot(v,p/1000,'g',linewidth=2)
#~~~~~~~~~~~~~~~~~~~~~~~~~
# Process 4-1
#~~~~~~~~~~~~~~~~~~~~~~~~~
v=linspace(v4,v1,100)
p=c2/v
plot(v,p/1000,'m',linewidth=2)
title('Ericsson Cycle',size='xx-large',color='k')
xlabel('Volume (m$^3$)')
ylabel('Pressure (kPa)')
+
# axis([0.0,v1+0.01,p_min/1000-100,p_max/1000+100])
# grid(linestyle='--',color='k')
text(v1,p1/1000-80,'1')
text(v2,p2/1000-80,'2')
text(v3-0.015,p3/1000-20,'3')
text(v4+0.01,p4/1000-20,'4')
data={'p':[p1,p2,p3,p4],
'v':[v1,v2,v3,v4],
'c':[c1,'' ,c2,"" ],
'State': [1,2,3,4]}
df=DataFrame(data)
savefig('Ericsson_final.jpg')
return df.set_index('State')
erc=ericsson(2*10**5,20*10**5,0.5,5,1.4)
show()
erc
输出
对于 $\mathrm{p_{min} \: = \: 2 \: \times \: 10^{5} \: Pa \:, \: p_{max} \: = \: 20 \: \times \: 10^{5} \: Pa \:, \: v_{max} \: = \: 0.5 \: m^{3} \:, \: r \: = \: 5 \: and \: \gamma \: = \: 1.4}$,从代码获得的结果如下图所示 −

此外,循环过程中不同点处的压力和体积如下表所示 −
State |
p |
v |
|---|---|---|
1 |
200000 |
0.50 |
2 |
200000 |
0.10 |
3 |
2000000 |
0.01 |
4 |
2000000 |
0.05 |
结论
本教程使用 Python 建模了爱立信和斯特林循环。文中介绍了开发这些循环函数的详细算法和编程步骤。

