用 Python 建模泰勒表方法
泰勒表方法是一种非常高效且优雅的方法,用于在考虑特定模板尺寸的情况下获得特定导数的有限差分方案。要理解它,必须非常清楚什么是模板。
假设想要评估 $\mathrm{\frac{d^{2}f}{dx^{2}}}$,那么在有限差分方法中,起点是泰勒级数。为了更好地理解该方法,请考虑下图。
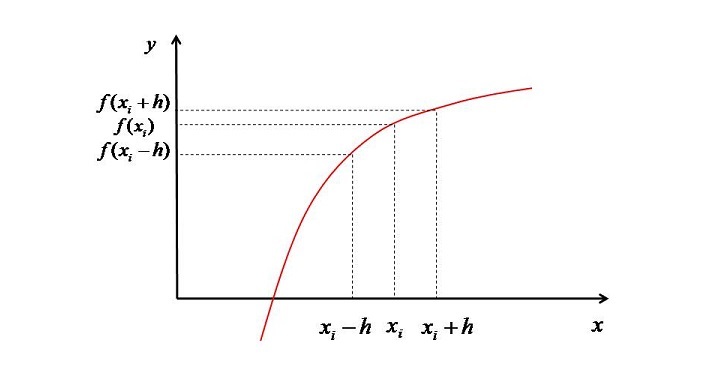
点 $\mathrm{x_{i} \: + \: h}$ 处的泰勒级数展开式为:
$$\mathrm{f(x_{i} \: + \: h) \: = \: f(x_{i}) \: + \: hf'(x_{i}) \: + \: \frac{h^{2}}{2!}f''(x_{i}) \: + \:\frac{h^{3}}{3!}f'''(x_{i}) \: + \:\frac{h^{3}}{3!}f'''(x_{i}) \: + \: \dotso}$$
$$\mathrm{f(x_{i} \: − \: h) \: = \: f(x_{i}) \: − \: hf'(x_{i}) \: + \: \frac{h^{2}}{2!}f''(x_{i}) \: − \:\frac{h^{3}}{3!}f'''(x_{i}) \: + \:\frac{h^{3}}{3!}f'''(x_{i}) \: − \: \dotso}$$
让我们将上述两个方程相加,并分离出包含二阶导数的项:
$$\mathrm{f''(x_{i}) \: = \: \frac{f(x_{i} \: + \: h) \: − \: 2f(x_{i}) \: + \: f(x_{i} \: − \: h)}{h^{2}}}$$
现在这是考虑点的二阶导数近似值$\mathrm{f(x_{i} \: + \: h) \: , \: f(x_{i})}$,以及 $\mathrm{f(x_{i} \: − \: h)}$。这就是我们所说的模板。模板基本上是点的集合,我们可以基于这些点用数字近似导数。现在为了简化书写任务,每当我必须写 $\mathrm{f(x_{i})}$ 时。我将把它简单地写成 $\mathrm{f_{i}}$,同样,我将把 $\mathrm{f(x_{i} \: − \: h)}$ 写成 $\mathrm{f_{i − 1}}$,等等。
现在这很容易,但是当任务是考虑模板中的非常多的点,并且必须以数字方式获得该模板某些导数的表达式时,问题就会变得非常复杂和困难。假设我需要根据模板 $\mathrm{f_{i} \: , \: f_{i+1} \: , \: f_{i+2} \: , \: f_{i+3}}$ 获得三阶导数 $\mathrm{(f'''(x_{i}))}$。那么这项任务将变得非常繁琐和耗时。因此,为了简化任务,泰勒表方法变得非常方便。
该方法可以很容易地解释如下:
首先,按如下方式写出导数:
$$\mathrm{f'''(x_{i}) \: = \: a \: f_{i} \: + \: b \: f_{i+1} \: + \: c \: f_{i+2} \: + \: d \: f_{i+3}}$$
现在的任务是找到 a、b、c 和 d。我们将导数及其系数按表格形式排列如下。

以黄色突出显示的单元格将由与 $\mathrm{1^{st}}$ 列中显示的模板相对应的泰勒级数系数填充。在红色突出显示的单元格中,我们将放置 0,除了与 $\mathrm{f'''(x_{i})}$ 相对应的单元格。
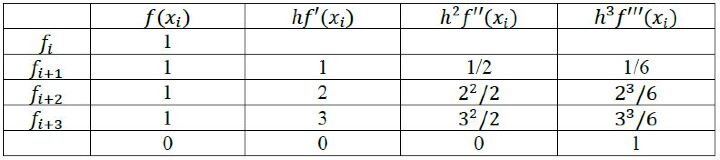
第一行乘以 a,第二行乘以 b,第三行乘以 c,第四行乘以 d,然后全部相加并等于最后一列(考虑维数)以获得以下等式:
$$\mathrm{a \: + \: b \: + \: c \: + \: d \: = \: 0}$$
$$\mathrm{(0 \: + \: b \: + \: 2c \: + \: 2d) \: = \: 0/h}$$
$$\mathrm{(0 \: + \: b/2 \: + \: 2c \: + \: 9d/2) \: = \: 0/h^{\wedge}2}$$
$$\mathrm{(0 \: + \: b/6 \: + \: 4c/3 \: + \: 9d/2) \: = \: 0/h^{\wedge}3}$$
现在这些可以很容易地排列成矩阵形式,这很容易解决。但这仍然是一项非常繁琐的任务,如果模板尺寸进一步增加,那么将非常困难。因此,本文使用了 Python 编程来简化任务。
在 Python 中实现泰勒表
我们要做的第一件事是编写一个代码来获取泰勒级数的系数。一般来说,泰勒级数写成。
$$\mathrm{f(x_{i} \: + \: \beta h) \: = \: f(x_{i}) \: + \: \beta f'(x_{i})h \: + \: \frac{\beta^{2}}{2!}f''(x_{i})h^{2} \: + \: \frac{\beta^{3}}{3!}f'''(x_{i})h^{3} \: + \: \frac{\beta^{4}}{4!}f''''(x_{i})h^{4} \: + \: \dots}$$
因此,上述级数的第 $\mathrm{i^{th}}$ 个系数可以写成:$\mathrm{(\frac{\alpha^{i}}{i!})}$。因此,我们首先为其编写函数,如下所示:
导入模块
from numpy import *
from math import *
# 泰勒级数函数
def TSC(n,α):
"""
n: Number of terms in the series
α: coefficient of h
"""
# Empty array of coefficients
c=empty(n)
for i in range(n):
c[i]=α**i/factorial(i)
return c
函数 TSC 将接受级数中的项数和 $\mathrm{\alpha}$。
然后,我们将使用此函数获取不同模板元素的系数,即之前用黄色突出显示的泰勒表行。
为了演示它,假设我们要使用模板 $\mathrm{(f_{i-1} \: , \: f_{i}, \: and \: f_{i+1})}$ 来评估 $\mathrm{d^{2}f/dx^{2}}$。我们将形成一个模板数组,使其包含下面提到的代码中的元素:
$$\mathrm{f_{i} \: : \: 0}$$
$$\mathrm{f_{i − 1} \: : \: −1}$$
$$\mathrm{f_{i+1} \: : \: +1}$$
$$\mathrm{f_{i−2} \: : \: −2}$$
$$\mathrm{f_{i+3} \: : \: 3}$$
我们还将提供必须为的导数的顺序用泰勒表近似,然后使用for循环填充表中元素,如下:
# 模板设置说明 #================================# # 1. f_i --> 0 # 2. f_(i-1)-->-1 # 3. f_(i+1)--> 1 # 4. f_(i-2)-->-2 # 5. f_(i+2)--> 2 #================================# # 形成 Stencil 数组 st=array([-1,0,1]) # 要计算的导数的阶数 order=2 # 泰勒表中的行数和列数 nt=len(st) Taylor_Table=empty((nt,nt)) for i in range(nt): Taylor_Table[i,:]=TSC(nt,st[i]) Taylor_Table
The output will be as follows:
array([[1. , -1. , 0.5],
[1. , 0. , 0. ],
[1. , 1. , 0.5]])
现在必须按如下方式设置向量 b:
# 右侧向量 b=zeros(nt) # 根据给定的导数设置 b b[order]=1 b
这将返回以下输出:
$$\mathrm{array([0. \: , \: 0. \: , \: 1.])}$$
在设置向量时,我们确保给定导数正下方的向量应获得值 1。但泰勒表矩阵和向量无法按原样求解,因为它们不是正确形式,因此必须在应用任何内置矩阵求解方法之前对它们进行转置,然后按如下方式求解:
a=linalg.solve(transpose(Taylor_Table),transpose(b))
这将产生以下输出:
$$\mathrm{array([−0.5 \: , \: 0. \: , \: 0.5])}$$
然而,在最终答案中,我们应该将这些值除以 h 的一些适当幂。这是在以下代码的帮助下完成的:
for i in range(nt):
print(f"a[{i}] = {a[i]}/h^{order}")
因此,最终答案如下:
a[0] = 1.0/h^2 a[1] = -2.0/h^2 a[2] = 1.0/h^2
因此,导数可以写成:
$$\mathrm{f''(x_{i}) \: = \: a[0]f_{i-1} \: + \: a[1]f_{i} \: + \: a[2]f_{i+1}}$$
$$\mathrm{f''(x_{i}) \: = \: \frac{f(x_{i} \: + \: h) \: − \: 2f(x_{i}) \: + \: f(x_{i} \: − \: h)}{h^{2}}}$$
完整代码如下:
# 导入模块
from numpy import *
from math import *
# 泰勒级数函数
#================================#
def TSC(n,α):
"""
n: Number of terms in the series
α: coefficient of h
"""
# Empty array of coefficients
c=empty(n)
for i in range(n):
c[i]=α**i/factorial(i)
return c
#================================#
# Instruction for setting stencil
# 1. f_i --> 0
# 2. f_(i-1)-->-1
# 3. f_(i+1)--> 1
# 4. f_(i-2)-->-2
# 5. F1_(i+2)--> 2
#================================#
# 形成 Stencil 数组
st=array([-1,0,1])
# 导数项的阶数
order=2
# 泰勒表中的行数和列数
nt=len(st)
Taylor_Table=empty((nt,nt))
for i in range(nt):
Taylor_Table[i,:]=TSC(nt,st[i])
Taylor_Table
#================================#
# 右侧向量
b=zeros(nt)
# 根据给定的导数设置 b
b[order]=1
#===============================#
# 求解矩阵
a=linalg.solve(transpose(Taylor_Table),transpose(b))
#=================================#
# 打印最终答案
for i in range(nt):
print(f"a[{i}] = {a[i]}/h^{order}")
#=================================#
在上面的代码中,我们只需更改行号中的模板和顺序即可。 33 和 36。
让我们解决介绍部分中提到的问题。
$$\mathrm{f'''(x_{i}) \: = \: a[0]f_{i} \: + \: a[1]f_{i+1} \: + \: a[2]f_{i+2} \: + \: a[3]f_{i+3}} $$
这里的模板将是:st=array([0,1,2,3]),顺序将是 3。程序输出将如下所示:
a[0] = -1.0/h^3 a[1] = 3.0/h^3 a[2] = -3.0/h^3 a[3] = 1.0/h^3
结论
在本教程中,使用 Python 编程实现了泰勒表方法。此外,首先解释了该方法,然后解释了 Python 策略。

