编译器设计 - 自上而下的解析器
我们在上一章中了解到,自上而下的解析技术会解析输入,并从根节点开始构建解析树,逐渐向下移动到叶节点。自上而下的解析类型如下所示:
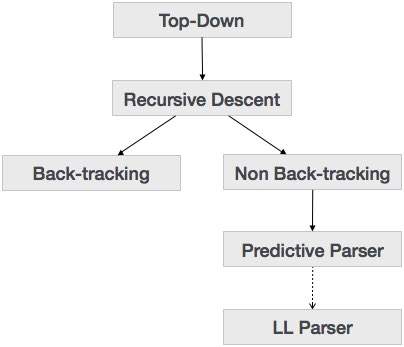
递归下降解析
递归下降是一种自上而下的解析技术,它从顶部构建解析树,并从左到右读取输入。它对每个终端和非终端实体使用程序。这种解析技术以递归方式解析输入以生成解析树,这可能需要也可能不需要回溯。但与其相关的语法(如果没有左因子分解)无法避免回溯。一种不需要任何回溯的递归下降解析形式称为预测解析。
这种解析技术被认为是递归的,因为它使用本质上是递归的上下文无关语法。
回溯
自上而下的解析器从根节点(起始符号)开始,并将输入字符串与生成规则进行匹配以替换它们(如果匹配)。要理解这一点,请看以下 CFG 示例:
S → rXd | rZd X → oa | ea Z → ai
对于输入字符串:read,自上而下的解析器将表现如下:
它将从生成规则中的 S 开始,并将其结果与输入的最左边的字母(即"r")进行匹配。 S 的生成规则 (S → rXd) 与其匹配。因此,自上而下的解析器前进到下一个输入字母(即"e")。解析器尝试扩展非终结符"X"并从左侧检查其生成规则 (X → oa)。它与下一个输入符号不匹配。因此,自上而下的解析器回溯以获取 X 的下一个生成规则 (X → ea)。
现在,解析器按顺序匹配所有输入字母。该字符串被接受。
|
|
|
|
|
预测解析器
预测解析器是一种递归下降解析器,它能够预测将使用哪个产生式来替换输入字符串。预测解析器不会受到回溯的影响。
为了完成任务,预测解析器使用前瞻指针,该指针指向下一个输入符号。为了使解析器免于回溯,预测解析器对语法施加了一些限制,并且只接受一类称为 LL(k) 语法的语法。

预测解析使用堆栈和解析表来解析输入并生成解析树。堆栈和输入都包含结束符号 $,表示堆栈为空且输入已被使用。解析器参考解析表来决定输入和堆栈元素的组合。

在递归下降解析中,解析器可能针对单个输入实例有多个生成式可供选择,而在预测解析器中,每个步骤最多只有一个生成式可供选择。可能存在没有与输入字符串匹配的生成式的情况,导致解析过程失败。
LL 解析器
LL 解析器接受 LL 语法。LL 语法是上下文无关语法的子集,但为了获得简化版本,有一些限制,以便于实现。 LL 语法可以通过两种算法实现,即递归下降或表驱动。
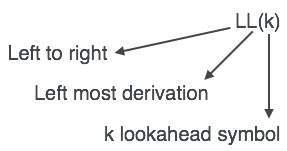
LL 解析器表示为 LL(k)。LL(k) 中的第一个 L 从左到右解析输入,LL(k) 中的第二个 L 代表最左推导,k 本身表示前瞻次数。通常 k = 1,因此 LL(k) 也可以写为 LL(1)。
LL 解析算法
我们可能坚持使用确定性 LL(1) 进行解析器解释,因为表的大小会随着 k 的值呈指数增长。其次,如果给定的语法不是 LL(1),那么通常,对于任何给定的 k,它都不是 LL(k)。
下面给出了 LL(1) 解析的算法:
Input:
string ω
parsing table M for grammar G
Output:
If ω is in L(G) then left-most derivation of ω,
error otherwise.
Initial State : $S on stack (with S being start symbol)
ω$ in the input buffer
SET ip to point the first symbol of ω$.
repeat
let X be the top stack symbol and a the symbol pointed by ip.
if X∈ Vt or $
if X = a
POP X and advance ip.
else
error()
endif
else /* X is non-terminal */
if M[X,a] = X → Y1, Y2,... Yk
POP X
PUSH Yk, Yk-1,... Y1 /* Y1 on top */
Output the production X → Y1, Y2,... Yk
else
error()
endif
endif
until X = $ /* empty stack */
如果 A → α | β 是 G 的两个不同产生式,则语法 G 为 LL(1):
对于无终结符,α 和 β 均会派生出以 a 开头的字符串。
α 和 β 中至多有一个可以派生出空字符串。
如果 β → t,则 α 不会派生出 FOLLOW(A) 中以终结符开头的任何字符串。


