有向加权图中从源到目标的单调最短路径
寻路算法基于图搜索技术,该技术研究节点之间的路径,从一个节点开始,通过连接逐步推进,直到达到目标。在本文中,我们将讨论加权图以及如何计算有向加权图中源节点和终端节点之间的单调最短路径。
什么是加权图?
加权图将图与权重函数结合在一起。也就是说,它为每条边分配一个整数权重。
图中边权重有多种用途 -
网络连接延迟
道路网络距离
社交网络互动的强度
表示权重的主要计算方法有两种 -
在邻接表中,为每个顶点注册边权重。
保留一个独特的 Set 数据结构,将每条边映射到其权重。
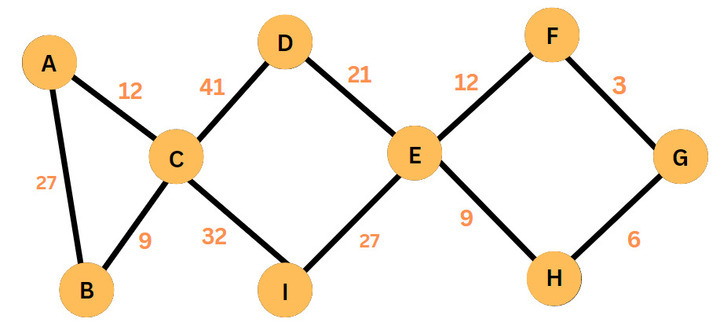
单调最短路径
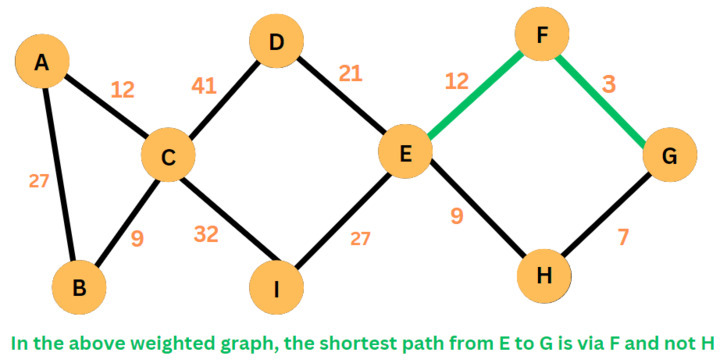
如果路径上每条边的权重严格递增或严格递减,则路径是单调的。
最短路径的性质是什么?
最短路径的性质如下:
权重并不总是距离。几何直觉很有用,但边权重表示时间或成本。
最短的路总是最简单的。
负权重会使事情复杂化。现在,我们假设边权重为正(或零)。
路径是定义的。最短路径必须保持边的方向。
并非所有顶点都必须可访问。如果一个节点无法从另一个节点访问,则不存在路径。因此,从 s 到 t 没有最短路径。
单个顶点或节点与其他顶点或节点之间可能存在多条权重最低的路径。
可能存在平行边和自环。
Dijkstra 最短路径算法
此方法首先确定起始节点与所有直接链接节点之间的最低权重关系。它会跟踪每个权重,并找到"最近"的节点。然后重复计算,但这次是从原始节点开始的累计总和。此过程始终如此,评估所有增量权重,并始终选择到目标节点的最小权重累计路径。
所有对最短路径 (APSP) 算法
此算法用于查找连接任意两个节点的最小距离路径。它比对网络的每两个顶点执行一次 SSSP 方法更快。
APSP 通过维护已确定权重的数量来改进流程,从而同时执行多个顶点。这些确定的权重用于查找到未知顶点的最短路径。
何时可以使用"所有对最短路径"?
当最短路径受阻或并非最优时,"所有对最短路径"通常用于探索备选方向。例如,在逻辑路线规划中,此方法可确保为多样性路由提供最优的众多路径。在评估所有或大多数节点之间的所有替代路径时,请使用 APSP。
单源最短路径 (SSSP)
"SSSP 算法"在主节点和网络中的每个节点之间找到一条"最短加权路径"。
它是如何工作的?
它的工作原理如下:
一切都从根节点开始,所有路径都从根节点开始评估。
选择来自根节点的具有最小权重的链接并将其与其关联节点合并到树中。
选择从根节点到每个具有最小累积权重的未访问节点的下一个关系,并以类似的方式将其放入树中。
一旦没有更多节点可放置,该过程就完成了,并获得了 SSSP。
何时可以应用此算法?
当需要确定从已确定的初始位置到所有其他节点的最佳路径时,可使用 SSSP 算法。由于路线由从根节点开始的整体路径权重决定,因此它有助于确定到每个节点的最佳路径,但当必须一次访问所有节点时,它并非总是必要的。
有向加权图中从源到目的地的单调最短路径
按照以下说明解决问题 -
对递增路径和递减路径分别运行两次 Dijkstra 算法。
如果节点之间的边权重小于指向源节点的最近距离路径的边权重,则使用"Dijkstra 递减最短路径算法"会更新从一个节点到另一个节点的最短路径。
同样适用于增长最短路径 - 仅当边比通往源的最短距离路线的边长时,才更新从一个节点到另一个节点的最短路径。
如果尚未到达目标顶点,则不存在合法的最短路径。
如果 Dijkstra 算法对增长和下降最短路径的遍历均未提供可行路径,则返回 -1。
示例
#include <bits/stdc++.h>
#include <limits>
#include <queue>
#include <vector>
using namespace std;
// 表示图中的一个顶点
class Vertex {
public:
int id;
vector<int> adj_list;
vector<double> adj_weights;
// 接受顶点 ID 的构造函数
Vertex(int num)
: id(num){
}
};
// 使用 Dijkstra 算法寻找单调最短路径
double shortest_path(vector<Vertex>& vertices, int src, int destination){
int N = vertices.size() - 1;
// 存储与 src 的距离以及与 src 最短路径上的边
vector<double> distTo(N + 1, numeric_limits<double>::max());
vector<double> edgeTo(N + 1, numeric_limits<double>::max());
// 将 src 的初始距离设置为最高值
for (int i = 1; i <= N; i++) {
distTo[i] = numeric_limits<double>::max();
}
// Dijkstra 的单调递减过程
distTo[src] = 0.0;
edgeTo[src] = numeric_limits<double>::max();
priority_queue<pair<double, int>,
vector<pair<double, int> >,
greater<pair<double, int> > >
pq;
pq.push(make_pair(0.0, src));
while (!pq.empty()) {
// 取当前距离 src 最近的顶点
pair<double, int> top = pq.top();
pq.pop();
int closest = top.second;
for (int i = 0; i < vertices[closest].adj_list.size(); i++) {
int neighbor = vertices[closest].adj_list[i];
double weight = vertices[closest].adj_weights[i];
// 检查边是否减少以及当前有向边是否会创建更短的路径
if (weight < edgeTo[closest] && distTo[closest] + weight < distTo[neighbor]) {
edgeTo[neighbor] = weight;
distTo[neighbor] = distTo[closest] + weight;
pq.push(make_pair(distTo[neighbor], neighbor));
}
}
}
// 存储 Dijkstra 算法第一遍的结果
double first_pass = distTo[destination];
// Dijkstra 算法的单调递增遍历
for (int i = 1; i <= N; i++) {
distTo[i] = numeric_limits<double>::max();
}
distTo[src] = 0.0;
edgeTo[src] = 0.0;
pq.push(make_pair(0.0, src));
while (!pq.empty()) {
// 取当前距离 src 最近的顶点
pair<double, int> top = pq.top();
pq.pop();
int closest = top.second;
for (int i = 0; i < vertices[closest].adj_list.size(); i++) {
int neighbor = vertices[closest].adj_list[i];
double weight = vertices[closest].adj_weights[i];
// 检查边是否在增加,以及当前有向边是否会创建更短的路径
if (weight > edgeTo[closest] && distTo[closest] + weight < distTo[neighbor]) {
edgeTo[neighbor] = weight;
distTo[neighbor] = distTo[closest] + weight;
pq.push(make_pair(distTo[neighbor], neighbor));
}
}
}
// 存储第二遍 Dijkstra 算法的结果
double second_pass = distTo[destination];
if (first_pass == DBL_MAX && second_pass == DBL_MAX)
return -1;
return min(first_pass, second_pass);
}
// 驱动代码
int main(){
int N = 6, M = 9, src, target;
// 创建 N 个顶点,编号为 1 到 N
vector<Vertex> vertices(N + 1, Vertex(0));
for (int i = 1; i <= N; i++) {
vertices[i] = Vertex(i);
}
// 向图中添加 M 条边
vertices[1].adj_list.push_back(3);
vertices[1].adj_weights.push_back(1.1);
vertices[1].adj_list.push_back(5);
vertices[1].adj_weights.push_back(2.0);
vertices[1].adj_list.push_back(6);
vertices[1].adj_weights.push_back(3.3);
vertices[2].adj_list.push_back(5);
vertices[2].adj_weights.push_back(2.7);
vertices[3].adj_list.push_back(4);
vertices[3].adj_weights.push_back(2.0);
vertices[3].adj_list.push_back(5);
vertices[3].adj_weights.push_back(1.1);
vertices[4].adj_list.push_back(2);
vertices[4].adj_weights.push_back(2.3);
vertices[5].adj_list.push_back(6);
vertices[5].adj_weights.push_back(2.4);
vertices[6].adj_list.push_back(2);
vertices[6].adj_weights.push_back(3.0);
//源顶点和目标顶点
src = 1;
target = 2;
double shortest = shortest_path(vertices, src, target);
cout << shortest << endl;
return 0;
}
输出
根据以上代码 -
5.4
在加权图中查找最短路径的替代方法
"Bellman-Ford 算法"代表一种"单源最短路径"技术。这意味着,给定一个加权网络,该方法将提供跨任意两个顶点的最小距离路径。
与 Dijkstra 算法相比,Bellman-Ford 算法可以对具有负权重边的图进行操作。因此,许多人更喜欢 Bellman-Ford 算法。
动态规划的示例包括此算法。它从单个节点开始,然后计算使用一条边可以访问的其他顶点之间的距离。然后,它继续搜索包含两条边的路径,并继续该过程。 Bellman-Ford 算法采用自下而上的策略。
结论
寻路算法可以帮助我们理解数据之间的联系。运行两次 Dijkstra 算法可以找到源节点和目标节点之间距离最小的路径。该方法使用边权重来找到一条路径,以降低源节点和所有其他节点之间的总权重。

