网络理论 - 耦合电路

当电路中的线圈（或电感器）之间存在互感时，该电路被称为耦合电路。线圈不过是电阻器和电感器的串联组合。如果没有电阻器，线圈就变成电感器。有时，术语线圈和电感器可以互换使用。

在本章中，我们首先讨论点约定，然后讨论耦合的分类。

点约定

点约定是一种技术，它提供有关点端子处电压极性的详细信息。在编写 KVL 方程时，此信息很有用。

• 如果电流从一个线圈（或电感器）的虚线端进入，则它会在另一个线圈（或电感器）处感应出电压，该电压在虚线端具有正极性。

• 如果电流从一个线圈（或电感器）的虚线端流出，则它会在另一个线圈（或电感器）处感应出电压，该电压在虚线端具有负极性。

耦合的分类

我们可以将耦合分为以下两类。

• 电耦合
• 磁耦合

现在，让我们讨论一下每个逐一耦合类型。

电耦合

当两个线圈（或电感器）之间存在物理连接时，就会发生电耦合。这种耦合可以是辅助类型，也可以是反向类型。它取决于电流是从虚线端进入还是从虚线端流出。

辅助型耦合

考虑以下电路，该电路具有两个串联连接的电感器。

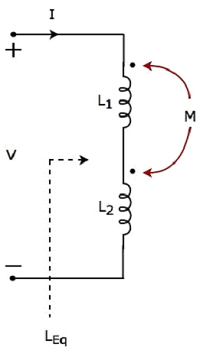
由于两个电感器串联连接，相同的电流I流过具有自感L₁和L₂的两个电感器。

在这种情况下，电流I从每个电感器的虚线端进入。因此，由于另一个线圈中流动的电流，每个电感器中的感应电压在虚线端将具有正极性。

在上述电路或网络的环路周围应用KVL。

$$V - L_1 \frac{dI}{dt} - M \frac{dI}{dt} - L_2 \frac{dI}{dt} - M \frac{dI}{dt} = 0$$

$$V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} + 2M \frac{dI}{dt}$$

$$V = (L_1 + L_2 + 2M)\frac{dI}{dt}$$

上式的形式为 $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$

因此，上图所示电感器串联组合的等效电感为

$$L_{Eq} = L_1 + L_2 + 2M$$

此时，等效电感增加了 2M。因此，上述电路是辅助型电耦合的一个例子。

反向型耦合

考虑以下电路，该电路具有两个串联的电感器。

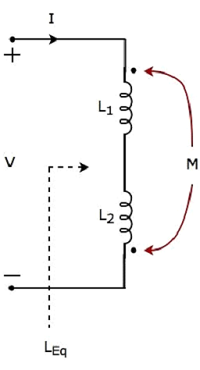
在上述电路中，电流I进入电感为L₁的电感器的虚线端。因此，它在电感为L₂的另一个电感器中感应出电压。因此，感应电压的正极性出现在该电感器的虚线端。

在上述电路中，电流I从电感为L₂的电感器的虚线端流出。因此，它会在电感为L₁的另一个电感器中感应出电压。因此，感应电压的负极性出现在该电感器的虚线端。

在上述电路或网络的环路周围施加KVL。

$$V - L_1 \frac{dI}{dt} + M \frac{dI}{dt} - L_2 \frac{dI}{dt} + M \frac{dI}{dt} = 0$$

$$\Rightarrow V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} - 2M \frac{dI}{dt}$$

$$\Rightarrow V = (L_1 + L_2 - 2M)\frac{dI}{dt}$$

上述方程的形式为$\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$

因此，上图所示电感器串联组合的等效电感为

$$L_{Eq} = L_1 + L_2 - 2M$$

在这种情况下，等效电感减少了 2M。因此，上述电路是电耦合的一个例子，属于反向类型。

磁耦合

当两个线圈（或电感器）之间没有物理连接时，就会发生磁耦合。这种耦合可以是辅助类型，也可以是反向类型。它取决于电流是从虚线端进入还是从虚线端离开。

辅助耦合

考虑以下变压器的等效电路。它有两个线圈，分别称为初级线圈和次级线圈。

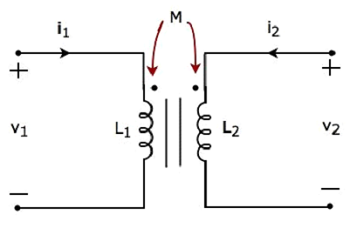
流过初级线圈和次级线圈的电流分别为 i₁ 和 i₂。在这种情况下，这些电流从相应线圈的虚线端进入。因此，由于电流流过另一个线圈，每个线圈中的感应电压在虚线端将具有正极性。

在初级线圈周围应用KVL。

$$v_1 - L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt} = 0$$

$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt}$公式 1

在次级线圈周围应用KVL。

$$v_2 - L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt} = 0$$

$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt}$等式 2

在公式 1 和公式 2 中，自感电压和互感电压具有相同的极性。因此，上述变压器电路是磁耦合的示例，属于辅助类型。

反向耦合

考虑以下变压器的电气等效电路。

流过初级和次级线圈的电流分别为 i₁ 和 i₂。在这种情况下，电流 i₁ 进入初级线圈的点端子。因此，它在次级线圈中感应出电压。因此，感应电压的正极性出现在次级线圈的虚线端。

在上述电路中，电流 i₂ 从次级线圈的虚线端流出。因此，它在初级线圈中感应出电压。因此，感应电压的负极性存在于该初级线圈的虚线端。

在初级线圈周围施加KVL。

$$v_1 - L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt} = 0$$

$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt}$公式 3

在次级线圈周围施加KVL。

$$v_2 - L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt} = 0$$

$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt}$等式 4

在等式 3 和等式 4 中，自感电压和互感电压具有相反的极性。因此，上述变压器电路是磁耦合的一个例子，属于相反类型。