网络拓扑矩阵
在上一章中,我们讨论了如何将电路转换为等效图。现在,让我们讨论网络拓扑矩阵,它对于使用等效图解决任何电路或网络问题都很有用。
与网络图相关的矩阵
以下是图论中使用的三个矩阵。
- 关联矩阵
- 基本环路矩阵
- 基本割集矩阵
关联矩阵
关联矩阵表示给定电路或网络的图。因此,可以从关联矩阵绘制出相同电路或网络的图形。
我们知道图形由一组节点组成,这些节点通过一些分支连接。因此,将分支连接到节点称为关联。关联矩阵用字母 A 表示。它也被称为节点到分支关联矩阵或节点关联矩阵。
如果在有向图中有"n"个节点和"b"个分支,则关联矩阵将具有"n"行和"b"列。这里,行和列对应于有向图的节点和分支。因此,关联矩阵的阶将为n × b。
关联矩阵的元素将具有以下三个值之一:+1、-1 和 0。
如果分支电流从选定节点离开,则元素的值将为 +1。
如果分支电流正进入选定节点,则元素的值将为 -1。
如果分支电流既不进入选定节点也不从选定节点离开,则元素的值将为 0。
查找关联矩阵的过程
按照以下步骤查找有向图的关联矩阵。
在给定的有向图中一次选择一个节点,并填写与该节点相对应的关联矩阵元素的值行。
对给定有向图的所有节点重复上述步骤。
示例
考虑以下有向图。
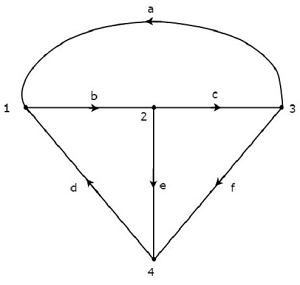
与上述有向图相对应的关联矩阵将是
$$A = \begin{bmatrix}-1 & 1 & 0 & -1 & 0 & 0\0 & -1 & 1 & 0 & 1 & 0\1 & 0 & -1 & 0 & 0 & 1 \0 & 0 & 0 & 1 & -1 & -1 \end{bmatrix}$$
上述矩阵的行和列表示给定有向图的节点和分支。此关联矩阵的阶为 4 × 6。
通过观察上述关联矩阵,我们可以得出结论,关联矩阵的列元素的和等于零。这意味着,分支电流从一个节点离开并只在另一个节点进入。
注意 − 如果给定的图是无向类型,则通过表示其每个分支上的箭头将其转换为有向图。我们可以考虑每个分支中电流的任意方向。
基本循环矩阵
基本循环或f 循环是一个循环,它只包含一个链接和一个或多个分支。因此,f 循环的数量将等于链接的数量。基本循环矩阵用字母 B 表示。它也被称为基本电路矩阵和 Tie-set 矩阵。该矩阵给出了分支电流和链接电流之间的关系。
如果在有向图中有"n"个节点和"b"个分支,则对应于给定图的选定树的共树中存在的链接数将为 b-n+1。
因此,基本循环矩阵将具有"b-n+1"行和"b"列。这里,行和列对应于给定图的共树和分支的链接。因此,基本循环矩阵的阶数将为(b - n + 1) × b。
基本循环矩阵的元素将具有以下三个值之一:+1、-1 和 0。
对于所选 f 循环的链接,元素的值将为 +1。
对于不属于所选 f 循环的其余链接和树枝,元素的值将为 0。
如果所选 f 循环的树枝电流方向与 f 循环链接电流方向相同,则元素的值将为 +1。
如果所选 f 循环的树枝电流方向与 f 循环链接电流方向相反,则元素的值将为 -1。
查找基本循环矩阵的过程
按照以下步骤查找基本给定有向图的循环矩阵。
选择给定有向图的树。
通过一次包含一个链接,我们将获得一个 f 循环。将与此 f 循环对应的元素的值填充到基本循环矩阵的一行中。
对所有链接重复上述步骤。
示例
查看以下有向图的树,该树被视为关联矩阵。
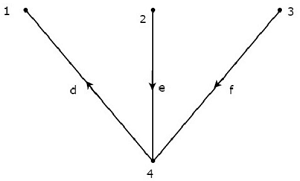
上述树包含三个分支 d、e 和 f。因此,分支 a、b 和 c 将是与上述树相对应的 Co-Tree 的链接。通过一次将一个链接添加到上述树中,我们将获得一个 f-loop。因此,由于有三个链接,因此将有三个 f-loop。这三个 f-loop 如下图所示。
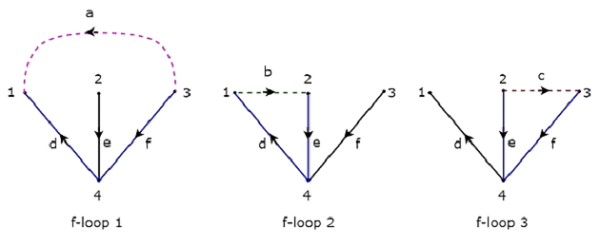
在上图中,用彩色线表示的分支形成 f-loop。我们将从每个 f-loop 中获得 Tie-set 矩阵的行元素值。因此,上述所考虑的树的 Tieset 矩阵 将是
$$B = \begin{bmatrix}1 & 0 & 0 & -1 & 0 & -1\0 & 1 & 0 & 1 & 1 & 0\0 & 0 & 1 & 0 & -1 & 1 \end{bmatrix}$$
上述矩阵的行和列表示给定有向图的链接和分支。此关联矩阵的阶为 3 × 6。
有向图的 基本循环矩阵 的数量将等于该有向图中的树的数量。因为,每棵树都会有一个基本循环矩阵。
基本割集矩阵
基本割集或f-割集是从图中删除的最小分支数,这样原始图将变成两个孤立的子图。f-割集仅包含一个树枝和一个或多个链接。因此,f-割集的数量将等于树枝的数量。
基本割集矩阵用字母 C 表示。该矩阵给出了分支电压和树枝电压之间的关系。
如果在有向图中有"n"个节点和"b"个分支,则给定图的选定树中存在的树枝数将为 n-1。因此,基本割集矩阵将有"n-1"行和"b"列。这里,行和列对应于所选树的树枝和给定图的分支。因此,基本割集矩阵的阶将为(n-1) × b。
基本割集矩阵的元素将具有以下三个值之一:+1、-1 和 0。
对于所选 f-cutset 的树枝,元素的值将为 +1。
对于不属于所选 f-cutset 的其余树枝和链接,元素的值将为 0。
如果所选 f-cut set 的链接电流方向与 f-cutset 树枝电流方向相同,则元素的值将为 +1。
如果所选 f-cut set 的链接电流方向与 f-cutset 树枝电流方向相反,则元素的值将为 -1。
查找基本割集矩阵的过程
按照以下步骤查找给定有向图的基本割集矩阵。
选择给定有向图的树并用虚线表示链接。
通过一次删除一个树枝和必要的链接,我们将得到一个 f 割集。将与此 f 割集相对应的元素值填充到基本割集矩阵的一行中。
对所有树枝重复上述步骤。
示例
考虑我们在关联矩阵部分讨论过的相同有向图。选择此有向图的分支 d、e 和 f 作为树枝。因此,剩余的分支 a、b 和此有向图的 c 将是链接。
下图中,树枝 d、e 和 f 用实线表示,链接 a、b 和 c 用虚线表示。
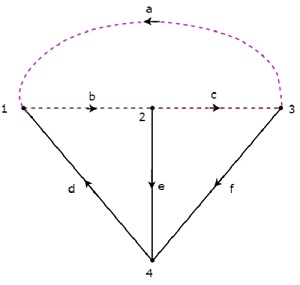
通过一次移除一个树枝和必要的链接,我们将得到一个 f 割集。因此,由于有三个树枝,因此将有三个 f 割集。这三个 f-cut 集 如下图所示。
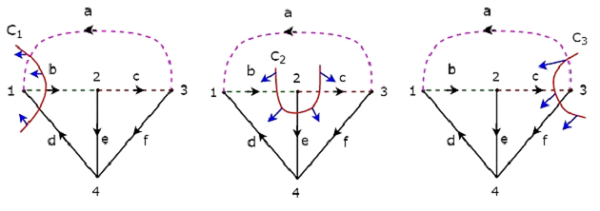
通过移除 C1、C2 和 C3 的一组枝条和链接,我们将得到三个 f-cut 集。我们将从每个 f-cut 集中获取基本割集矩阵的行元素值。因此,上述所考虑的树的基本割集矩阵将是
$$C = \begin{bmatrix}1 & -1 & 0 & 1 & 0 & 0\0 & -1 & 1 & 0 & 1 & 0\1 & 0 & -1 & 0 & 0 & 1 \end{bmatrix}$$
上述矩阵的行和列表示给定有向图的树枝和分枝。此基本割集矩阵的阶为 3 × 6。
有向图的基本割集矩阵的数量将等于该有向图中的树的数量。因为每棵树都有一个基本割集矩阵。

