等效电路示例问题

在上一章中，我们分别讨论了串联组合和并联组合的等效电路。在本章中，让我们通过考虑类似无源元件的串联和并联组合来解决一个示例问题。

示例

让我们找到以下电气网络端子 A 和 B 之间的等效电阻。

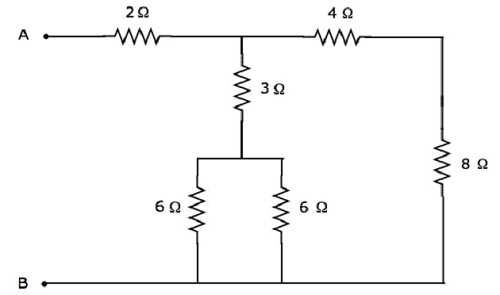
我们将通过将上述网络最小化为两个端子之间的单个电阻器来获得端子 A 和 B 之间的等效电阻。为此，我们必须识别串联和并联电阻的组合，然后在每一步中找到相应形式的等效电阻。

给定的电网络修改为下图所示的以下形式。

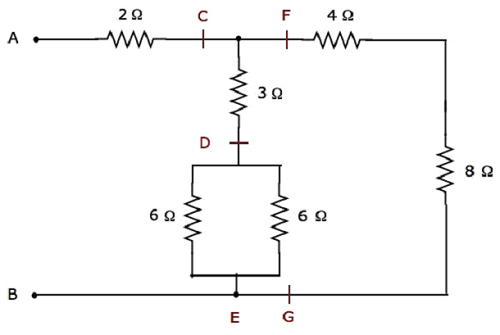
在上图中，字母 C 到 G 用于标记各种端子。

步骤 1 − 在上面的网络中，两个 6 Ω 电阻 以并联方式连接。因此，D 和 E 之间的等效电阻将为 3 Ω。这可以通过进行以下简化获得。

$$R_{DE} = \frac{6 imes 6}{6 + 6} = \frac{36}{12} = 3 \Omega$$

在上述网络中，电阻器4 Ω和8 Ω串联连接。因此，F和G之间的等效电阻将为12 Ω。这可以通过进行以下简化获得。

$$R_{FG} = 4 + 8 = 12 \Omega$$

步骤2 −下图显示了步骤 1 之后的简化电气网络。

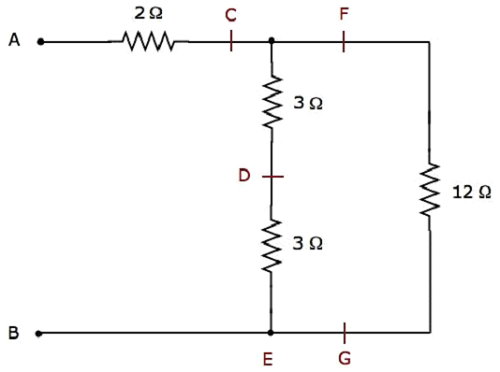
在上述网络中，两个 3 Ω 电阻 串联连接。因此，C 和 E 之间的等效电阻将为 6 Ω。这可以通过进行以下简化来获得。

$$R_{CE} = 3 + 3 = 6 \Omega$$

步骤 3 −下图显示了步骤 2 之后的简化电气网络。

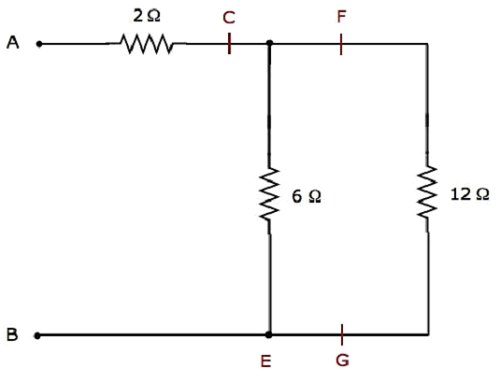
在上述网络中，电阻器6 Ω和12 Ω并联连接。因此，C 和 B 之间的等效电阻将为 4 Ω。这可以通过进行以下简化来获得。

$$R_{CB} = \frac{6 imes 12}{6 + 12} = \frac{72}{18} = 4 \Omega$$

步骤 4 −下图显示了步骤 3 之后简化的电气网络。

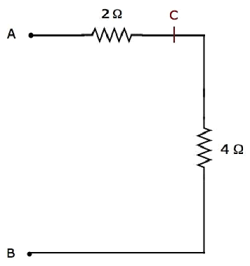
在上述网络中，电阻2 Ω和4 Ω串联在端子 A 和 B 之间。因此，A 和 B 之间的等效电阻为 6 Ω。这可以通过进行以下简化获得。

$$R_{AB} = 2 + 4 = 6 \Omega$$

因此，给定电气网络的端子 A 和 B 之间的等效电阻为6 Ω。