NumPy - 多项分布

什么是多项分布?

多项分布是二项分布的推广。它表示一系列实验中多个结果的概率，其中每次试验都有固定数量的结果，并且每个结果都有一个给定的概率。它由两个参数定义:

• n 试验次数。
• p 每个结果的概率列表或数组。概率之和必须等于 1。

例如，考虑掷一个六面骰子 10 次。多项分布可以帮助确定每张脸出现一定次数的概率。

在 NumPy 中生成多项样本

NumPy 提供了 numpy.random.multinomial() 函数，可以从多项分布中生成随机样本。此函数需要指定试验次数和每个结果的概率。

示例

此处，每一行代表单个实验的结果，显示每个结果的发生次数 -

import numpy as np

# 定义参数
# 试验次数
n = 10
# 4 种结果的概率
p = [0.1, 0.3, 0.4, 0.2]

# 生成样本
samples = np.random.multinomial(n, p, size=5)
print(samples)

以下是获得的输出 -

[[1 2 5 2]
[1 5 2 2]
[0 5 4 1]
[0 4 4 2]
[0 4 4 2]]

理解数学基础

多项分布的 PMF 根据给定参数计算特定结果的概率。数学上，它表示为 −

P(X1 = x1, ..., Xk = xk) = (n! / (x1! * ... * xk!)) * (p1x1) * ... * (pkxk)

其中，

• n:试验总数。
• p1, ..., pk:每种结果的概率。
• x1, ..., xk:每种结果的观测频率。

理解此公式有助于您解释结果并验证 NumPy 生成的样本。

模拟真实场景

多项式随机分布在现实世界中被广泛应用，例如选举结果、掷骰子和遗传概率。

让我们模拟几个例子来理解它的实际应用:

示例 1:模拟掷骰子

在本例中，我们模拟掷一个六面骰子 20 次，并计算每个面出现的频率 -

import numpy as np

# 模拟掷骰子
# 掷骰子次数
n = 20
# 每个面出现的概率相等
p = [1/6] * 6

# 生成结果
results = np.random.multinomial(n, p)
print("掷骰子频率:", results)

每个值代表实验中某个面出现的频率−

掷骰子频率:[5 2 5 5 3 0]

示例 2:预测选举结果

假设一场选举有三位候选人，我们想根据预测概率模拟 100 位选民的选择 -

import numpy as np

# 模拟选举结果
# 选民人数
n = 100
# 每位候选人的概率
p = [0.4, 0.35, 0.25]

# 生成选举模拟
results = np.random.multinomial(n, p)
print("每位候选人的得票数:", results)

这演示了多项分布如何在概率场景中使用 -

每位候选人的得票数:[48 31 21]

可视化多项分布

可视化是分析和解释数据的有效方法。使用 Matplotlib，我们可以绘制多项分布的结果以便更好地理解。

示例:多项结果的条形图

import numpy as np
import matplotlib.pyplot as plt

# 可视化结果
outcomes = ['结果 1', '结果 2', '结果 3', '结果 4']
frequencies = np.random.multinomial(50, [0.2, 0.3, 0.4, 0.1])

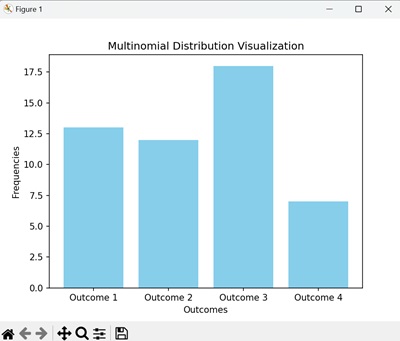
plt.bar(outcomes, frequencies, color='skyblue')
plt.title('多项分布可视化')
plt.xlabel('结果')
plt.ylabel('频率')
plt.show()

结果显示一个条形图，显示多项分布中每个结果的频率 -

比较多项分布和二项分布

二项分布处理两种可能的结果(例如成功和失败)，而多项分布则将其扩展到多种结果。

例如，二项分布可以模拟抛硬币，而多项分布可以模拟掷骰子或具有两种以上结果的分类数据。

主要区别

以下是多项分布和二项分布之间的主要区别−

• 结果数量:二项式有两个结果，而多项式有更多结果。
• 复杂性:多项式需要指定多个类别的概率。
• 应用:多项式更适用于涉及分类数据的场景。

自定义多项式模拟

NumPy 允许通过调整试验次数、概率和生成样本的大小等参数来灵活地自定义模拟。

让我们看一个示例，其中我们模拟了具有不同概率的多个实验。

示例:具有不同概率的多个模拟

以下示例演示了调整概率如何影响结果 −

import numpy as np

# 自定义概率
probabilities = [
[0.5, 0.3, 0.2],
[0.4, 0.4, 0.2],
[0.6, 0.2, 0.2]
]

for p in probabilities:
results = np.概率.multinomial(20, p)
print(f"Probabilities: {p} => {p})结果:{results}")

执行上述代码后，我们得到以下输出 -

概率:[0.5, 0.3, 0.2] => 结果:[ 9 10  1]
概率:[0.4, 0.4, 0.2] => 结果:[ 4 12  4]
概率:[0.6, 0.2, 0.2] => 结果:[12  4  4]