使用半加器设计全加器

在数据处理中，操作数的加法是计算机、计算器等不同电子设备执行的最基本操作之一。用于执行两个或多个数字(更具体地说是二进制数字)相加的电子电路称为加法器。众所周知，逻辑电路使用二进制数字系统执行操作，因此加法器也称为二进制加法器。

加法器的类型

根据加法器电路可以添加的二进制位数，加法器(或二进制加法器)有两种类型 −

• 半加器
• 全加器

在这里，我们将讨论使用半加器实现全加器。但在此之前，让我们先了解一下半加器和全加器的基础知识。

什么是半加器?

半加器是一种组合逻辑电路，用于将两个二进制数字相加。半加器提供输出以及进位(如果有)。半加器电路可以通过连接一个 XOR 门和一个 AND 门来设计。它有两个输入端和两个输出端，用于求和 (S) 和进位 (C)。半加器的框图和电路图如图 1 所示。

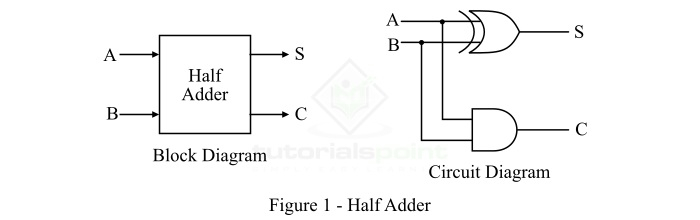
在半加器中，XOR 门的输出是两位之和，AND 门的输出是进位位。但在半加器电路中，一次加法得到的进位不会在下一次加法中转发。

半加器的输出方程为，

$$\mathrm{Sum, \: S \: = \: A \: \oplus \: B}$$

$$\mathrm{Carry, \: C \: = \: A \: \cdot \ B}$$

什么是全加器?

全加器也是一种组合逻辑电路，它可以将两个二进制数字(位)和一个进位位相加，并产生一个和位和一个进位位作为输出。

换句话说，设计用于将三个二进制数字相加并产生两个输出(和和进位)的组合电路称为全加器。因此，全加器电路将三个二进制数字相加，其中两个是输入，一个是从上一次加法转发的进位。全加器的框图和电路图如图 2 所示。

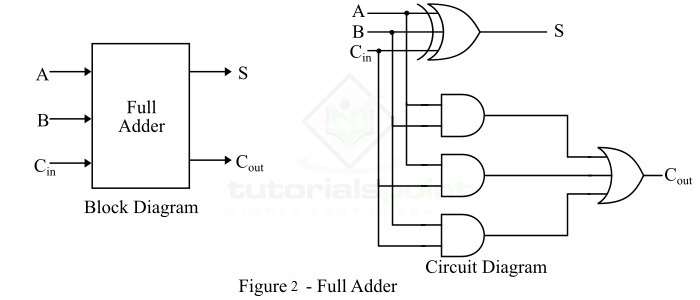
很明显，全加器的逻辑电路由一个 XOR 门、三个 AND 门和一个 OR 门组成，它们的连接方式如图 2 所示。这里，A和B是输入位，C_in是上一次加法的进位，S是和位，C_out是输出进位位。

全加器的输出方程为，

$$\mathrm{Sum, \: S \: = \: A \: \oplus \: B \: \oplus \: C_{in}}$$

$$\mathrm{Carry, \: C_{out} \: = \: Ab \: + \: AC_{in} \: + \: BC_{in}}$$

现在，让我们讨论使用半加法器

使用半加法器实现全加法器

使用两个半加法器的全加法器的逻辑图如图 3 所示 −

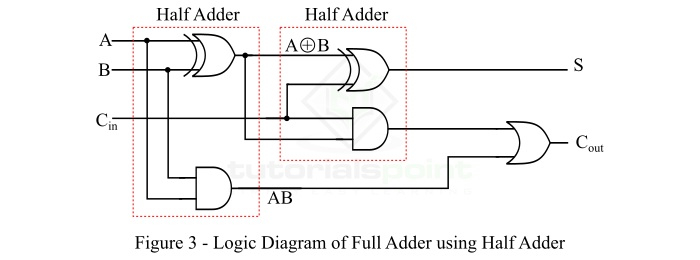
使用两个半加法器的全加法器的框图如图 4 所示。

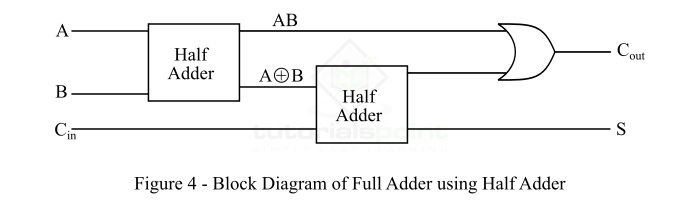
从使用半加法器的全加法器的逻辑图中可以看出，我们需要两个 XOR 门、两个 AND 门和一个 OR 门来实现使用半加器。

但是，使用半加器实现全加器有一个主要缺点，即增加了传播延迟。这意味着，输入位必须连续通过几个门，这会增加全加器电路的总传播延迟。