数字电子技术 - 德摩根定理
在布尔代数中,定义了一些规则来执行数字逻辑电路中的运算。布尔代数是一种对二进制数字(即 0 和 1)执行运算的工具。这两个二进制数字 0 和 1 用于表示数字电路在输入和输出端的 FALSE 和 TRUE 状态。由乔治布尔开发的布尔代数使用 0 和 1 来创建数字电路的真值表和逻辑表达式,如 AND、OR、NOT 等,用于分析和简化复杂电路。
还有另一位英国数学家奥古斯都·德摩根,他将 NAND 和 NOR 运算分别解释为 NOT AND 和 NOT OR 运算。这种解释被称为德摩根定理。在本教程中,我们将详细讨论德摩根定理。
什么是德摩根定理?
德摩根定理是布尔代数中的一个强大定理,它有一组两个规则或定律。这两条定律是为了展示两个变量 AND、OR 和 NOT 运算之间的关系而开发的。这两条规则使变量可以被否定,即与其原始形式相反。因此,德摩根定理给出了逻辑函数的对偶。
现在,让我们讨论德摩根定理的两个定律。
德摩根第一定理(定律 1)
德摩根第一定律指出,变量和(OR 运算)的补数等于它们各个补数的乘积(AND 运算)。换句话说,两个或多个变量的补码与每个单独变量的补码的与相等,即
$$\mathrm{\overline{A+B} \: = \: \bar{A} \cdot \bar{B}}$$
或者,也可以表示为,
$$\mathrm{\lgroup A \: + \: B \rgroup' \: = \: A'\cdot B'}$$
该定律左侧和右侧的逻辑实现如图1所示。
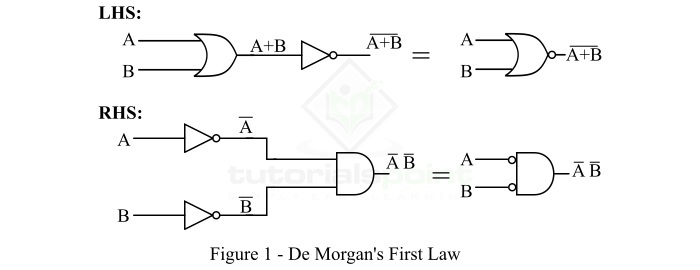
因此,德摩根第一定律证明 NOR 门等同于带气泡的 AND 门。以下真值表显示了该定律的证明。
| Left Side | Right Side | ||||
|---|---|---|---|---|---|
| Input | Output | Input | Output | ||
| A | B | (A + B)' | A' | B' | A'· B' |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
该真值表证明左边的布尔表达式等价于德摩根第一定律表达式右边的布尔表达式。
此外,德摩根定理第一定律可以扩展到任意数量的变量,或变量的组合。
例如,
$$\mathrm{\overline{A \: + \: B \: + \: C \: + \: D \: + \: E \: + \: \dotso} \: = \: \bar{A} \: \bar{B} \: \bar{C} \: \bar{D} \: \bar{E} \: \dotso}$$
另外,
$$\mathrm{\overline{ABC \: + \: DE \: + \: FGH \: + \: \dotso}\: = \: \overline{\lgroup ABC \rgroup}.\overline{\lgroup DE \rgroup}.\overline{\lgroup FGH\rgroup}.\dotso}$$
从以上讨论中,我们可以得出结论,德摩根第一定律将表达式从非符号下的和形式转换为乘积形式。
德摩根第二定理(定律2)
德摩根第二定律指出,变量乘积(AND 运算)的补数等于它们各自补数的和(OR 运算)。
换句话说,两个或多个 AND 运算变量的补数等于每个单独变量的补数之和,即
$$\mathrm{\overline{AB} \: = \: \overline{A} \: + \: \overline{B}}$$
也可以表示为,
$$\mathrm{\lgroup AB \rgroup' \: = \: A' \: + \: B'}$$
此左右两侧的逻辑实现表达式如图 2 所示。
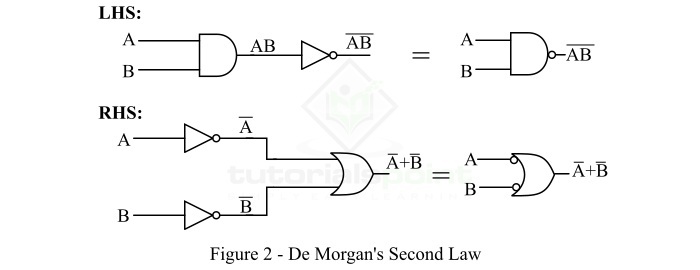
因此,德摩根第二定律证明 NAND 门等效于带气泡的 OR 门。以下真值表显示了该定律的证明。
| Left Side | Right Side | ||||
|---|---|---|---|---|---|
| Input | Output | Input | Output | ||
| A | B | AB | A' | B' | A' + B' |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 |
该真值表证明左边的布尔表达式等同于德摩根第二定律表达式右边的布尔表达式。
与第一定律类似,我们可以将德摩根第二定律扩展为任意数量的变量或变量组合。
例如,
$$\mathrm{\overline{ABCDE \dotso} \: = \: \overline{A} \: + \: \overline{B} \: + \: \overline{C} \: + \: \overline{D} \: + \: \overline{E} \: + \: \dotso}$$
并且,对于变量的组合,
$$\mathrm{\overline{\lgroup ABC \rgroup} \overline{\lgroup DE \rgroup} \overline{\lgroup FG \rgroup \dotso} \: = \: \overline{ABC} \: + \: \overline{DE} \: + \: \overline{FG}}$$
因此,从以上讨论中,我们可以得出结论,德摩根第二定律将变量的乘积形式或非符号下的变量组合转化为和的形式。
因此,德摩根定律将AND运算转化为OR运算,将OR运算转化为AND运算。这个原理称为对偶性。
示例 1
将德摩根定理应用于以下布尔表达式,
$$\mathrm{F \: = \: \overline{AB \overline{ \lgroup C \: + \: D \rgroup}EF}}$$
解决方案
给定表达式为,
$$\mathrm{F \: = \: \overline{AB \overline{ \lgroup C \: + \: D \rgroup}EF}}$$
由于给定表达式在 NOT 符号下具有 AND 运算,因此在应用德摩根第二定理时定律,我们得到,
$$\mathrm{F \: = \: \overline{AB} \: + \: \lgroup C \: + \: D \rgroup \: + \: \overline{EF}}$$
这是给定表达式的等价或对偶。
示例 2
将德摩根定理应用于以下布尔表达式,
$$\mathrm{F \: = \: \overline{AB \: + \: \overline{CD}}}$$
解决方案
给定表达式是,
$$\mathrm{F \: = \: \overline{AB \: + \: \overline{CD}}}$$
给定的表达式是 NOT 符号下的变量和的形式,因此应用德摩根第一定律,我们得到该表达式的对偶。
$$\mathrm{F \: = \: \overline{AB} \cdot \overline{\overline{CD}} \: = \: \overline{AB} \cdot CD}$$
在本章中,我们解释了德摩根定理的两个定律,并展示了它们如何有助于在数字逻辑电路中执行不同的操作。

