K-Map 中的无关条件

K-Map 或 卡诺图 是一种简化布尔表达式的图形方法。K-Map 由相邻的方块或单元格排列组成，其中每个单元格代表以和或乘积形式表示的特定变量组合。

在 K-map 方法中，有一个有用的条件，即 无关条件，它有助于简化布尔函数。无关条件使 K-map 中的变量分组变得容易。在本教程中，我们将借助已解决的示例来理解 K-map 简化中的"无所谓"概念。

有时，在某些输入组合的布尔表达式中，由于输入组合无效或输出的精确值不重要，因此未指定输出值。这些未指定布尔函数值的输入组合称为无所谓组合。 无关组合也称为可选组合。在 K-map 中，无关组合用"X"或"d"或"ϕ"表示。

例如，在 8421 二进制代码中，二进制组合 1010、1011、1100、1101、1110 和 1111 是无效项，其对应的输出是无关组合。类似地，在 Excess-3 代码中，组合 0000、0001、0010、1101、1110 和 1111 不会出现，因此这些组合被称为无关组合。

当我们处理 SOP(乘积和)K-map 时，如果每个无关项有助于减少表达式，则将其视为 1，否则将其视为 0 并保持不变。

另一方面，当我们使用 POS(和的乘积)K-map 时，如果每个无关项有助于减少表达式，则将其视为 0，否则将其视为 1 并保持不变。

此外，我们可以将带有无关项的标准乘积和 (SSOP) 表达式转换为标准和乘积 (SPOS) 表达式，方法是保持无关项不变，并写出缺失的最小项SSOP 形式作为 SPOS 形式的最大项。

类似地，我们可以将带有无关项的标准和积 (SPOS) 表达式转换为标准乘积和 (SSOP) 表达式，方法是保留 SPOS 表达式的无关项，并将 SPOS 表达式的缺失最大项写为 SSOP 表达式的最小项。

现在，让我们讨论一些已解决的示例，以了解 K-map 中的无关条件。

示例 1

使用 K-map 最小化以下 SOP 形式的 4 变量布尔表达式。

$$\mathrm{\mathit{f}\lgroup A,B,C,D\rgroup=\sum m \lgroup 0,1,4,5,6,10,13\rgroup +d \lgroup 2,3 \rgroup}$$

解决方案

给定布尔函数的 SOP K-map 表示如图 1 所示。

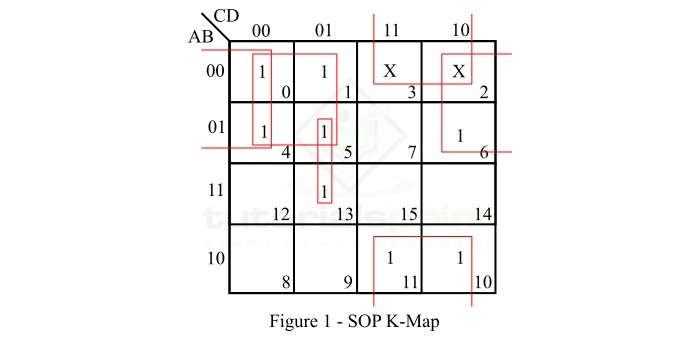
正如我们在给定表达式中看到的那样，有两个无关紧要的项在 K-map 上用 X 表示。

解释

表达式的简化按以下步骤进行 −

• 最小项 m₀、m₁、m₄ 和 m₅ 形成一个 4 平方。将其制作并读作 $\mathrm{\lgroup \bar{A} \: \bar{C}\rgroup}$。
• 最小项 m₁₀ 和 m₁₁ 形成一个 4 平方，其中有两个无关项 m₂ 和 m₃。将其写成 $\mathrm{\bar{B}C}$。
• 最小项 m₀、m₄、m₆ 和无关项 m₂ 一起构成一个 4 平方数。将其写成 $\mathrm{\bar{A} \: \bar{D}}$。
• 最小项 m₅ 和 m₁₃ 构成一个 2 平方数。将其写成 $\mathrm{B\bar{C}D}$。
• 最后，将所有乘积项写成 SOP 形式。

因此，最小布尔表达式为，

$$\mathrm{\mathit{f} \lgroup A,B,C,D \rgroup \: = \: \bar{A} \: \bar{C} \: + \: \bar{B}C \: + \: \bar{A} \: \bar{D} \: + \: B \bar{C}D}$$

示例2

使用 K 图最小化以下 POS 形式的 4 变量布尔表达式。

$$\mathrm{\mathit{f} \lgroup A,B,C,D \rgroup \: = \: \prod M \lgroup 1,5,6,12,13,14 \rgroup \: + \: d \lgroup 2,4 \rgroup}$$

解决方案

给定布尔函数的 POS K 图表示如图 2 所示。

表达式中有两个无关项，在 K-map 上用 X 表示。

解释

给定函数的约简按以下步骤进行 −

• 最大项 M₅、M₁₂ 和 M₁₃ 以及无关项 M₄ 形成一个 4 平方。将其制作并读作 $\mathrm{\bar{B} \: + \: C}$。
• 最大项 M₆、M₁₂ 和 M₁₄ 以及无关项 M₄ 形成一个 4 平方。将其写成 $\mathrm{\bar{B} \: + \: D}$。
• 最大项 M₁ 和 M₅ 形成一个 2 平方数。将其写成 $\mathrm{A \: + \: C \: + \: \bar{D}}$
• 将所有和项写成 POS 形式。

因此，最小布尔表达式为，

$$\mathrm{\mathit{f} \lgroup A,B,C,D \rgroup \: = \: \lgroup \bar{B} \: + \: C \rgroup \: + \: \lgroup \bar{B} \: + \: D \rgroup \: + \: \lgroup A \: + \: C \: + \: \bar{D} \rgroup}$$

结论

这都是关于 K-map 中的无关条件。正如我们在本教程以上部分所讨论的，不关心条件是一个重要且强大的概念，它有助于使用 K-map 最小化布尔函数。