数字电子技术 - 十六进制算术
什么是十六进制算术?
在数字电子技术中,十六进制数用于以更紧凑的形式表示二进制信息,因为一个十六进制数字可以表示一组 4 个二进制数字。因此,十六进制数及其算术运算在数字电子领域中起着至关重要的作用。
十六进制算术是一种数学系统,允许对十六进制或十六进制数执行加、减、乘、除等算术运算。
在本章中,我们将介绍以下四个基本的十六进制算术运算 −
- 十六进制加法
- 十六进制减法
- 十六进制乘法
- 十六进制除法
让我们借助示例详细了解每个十六进制算术运算。
十六进制加法
十六进制加法是对十六进制数执行的基本算术运算之一,用于确定其总和。基本上,十六进制加法与十进制加法类似。但在十六进制加法中,如果总和大于或等于 16,则会产生进位到下一个更高的列。
让我们看一些已解决的示例,以更好地理解十六进制加法。
示例 1
添加 (5A)16 和 (BF)16。
解决方案
给定十六进制数的加法如下所示 −
(5A)16 + (BF)16 = (119)16
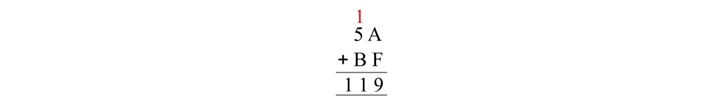
解释
首先将最右列的十六进制数字相加:A + F = 10 + 15 = 25 = 16 + 9。这里,16 形成进位到下一列。因此,总和为 9,1 作为进位到下一列。
移至下一列并将数字连同进位相加:5 + B + 1 = 5 + 11 + 1 = 17 = 16 + 1。这里,16 形成进位到下一列。因此,总和为 1,进位为 1。没有剩余数字,因此进位也将写为总和的最左边数字。
因此,5A 和 BF 的十六进制总和为 119。
示例 2
将 (ABC)16 和 (2A9)16 相加。
解决方案
给定数字的十六进制总和如下所示 −
(ABC)16 + (2A9)16 = (D65)16

解释
首先将最右列的数字相加:C + 9 = 12 + 9 = 21 = 16 + 1。这里,16 形成一个进位。因此,总和为 1,进位为 1。
移至下一列,并将数字与上一步中的进位相加:B + A + 1 = 11 + 10 + 1 = 22 = 16 + 6。因此,总和为 6,进位为 1 到下一列。
移至最左列,并将数字与上一步中的进位相加:A + 2 + 1 = 10 + 2 + 1 = 13。由于总和为 13,小于 16,因此不产生进位。在十六进制数系统中,字母 D 表示 13。
因此,ABC 和 2A9 的十六进制和 = D65。
这都是关于十六进制加法的,它涉及逐列添加给定十六进制数的数字。执行十六进制加法时要记住的最重要的一点是,当特定列中的和大于或等于 16(即十六进制数系统的基数)时,会产生进位到下一列。
十六进制减法
十六进制减法是对十六进制数执行的基本算术运算,以确定它们之间的差异。
十六进制减法类似于十进制减法。唯一的区别是,在十六进制减法中,当被减数小于被减数时,从高位数字借位 1,相当于 16。
让我们借助解题示例来理解十六进制减法。
示例 1
从 (A57)16 中减去 (125)16。
解决方案
给定十六进制数的减法如下所示 −
(A57)16 - (125)16 = (932)16
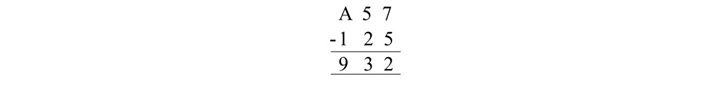
解释
从最右边的列开始减去十六进制数字:7 – 5 = 2。记下结果。
移至下一列并减去数字:5 – 2 = 3。记下数字 3 作为差值。
移至最左边的列并减去数字:A – 1 = 10 – 1 = 9。记下结果作为差值。
因此,A57 和 125 的十六进制差值为 932。
示例 2
从 (BC5)16 中减去 (1DA)16。
解决方案
BC5 和 1DA 的十六进制减法如下所示 −
(BC5)16 - (1DA)16 = (9EB)16

解释
首先从最右列的数字中减去:5 – A。由于 5 小于 A (10),所以我们必须从下一个高位数字借位。从下一列 (C) 借位后,数字 5 将变为 5 + 16(因为 16 相当于借位 1)= 21。因此,21 – A = 11 (B)。记下 B 作为差值。
移至下一列并减去数字:B – D。同样,B 小于 D,因此我们从高位数字 B 借位。借位后,B 将变为 B + 16 = 27。因此,27 – D = 14 (E)。将数字 E 记为差值。
移至最左边的列并减去数字:A – 1 = 9。记下结果。
因此,BC5 和 1DA 的十六进制差等于 9EB。
这些示例解释了两个十六进制数相减的过程。现在让我们讨论十六进制数的第三个基本算术运算,即十六进制乘法。
十六进制乘法
十六进制乘法是一种用于确定两个十六进制数乘积的算术运算。
十六进制乘法类似于十进制乘法。但是,在十六进制乘法的情况下,当乘积大于或等于 16 时,将产生进位到下一列。
以下示例演示了两个十六进制数相乘的过程。
示例 1
将 (A19)16 乘以 (B)16。
解决方案
给定十六进制数的乘法如下所示 −
(A19)16 乘以 (B)16 = (6F13)16

解释
将数字 (B)16 与数字 (A19)16 的每个数字相乘,并记下结果。
首先,我们将 B 乘以 9,得到 99 = 96 + 3。因此,3 写为乘积,96 写为进位 6(16 × 6 = 96)到下一列。
然后,我们将 B 乘以 1,并将进位 6 加到乘积中。得到 17 = 16 + 1。这里,结果是 1,进位是 1。
最后,我们将 B 乘以 A,并将上一步中的进位 1 加到乘积中。得到 96 + 15(十六进制中的 F)。结果为 F,进位 6。
因此,A19 和 B 的最终十六进制乘积为 6F13。
示例 2
将 (ABC)16 乘以 (29)16。
解决方案
给定十六进制数的乘法如下所示 −
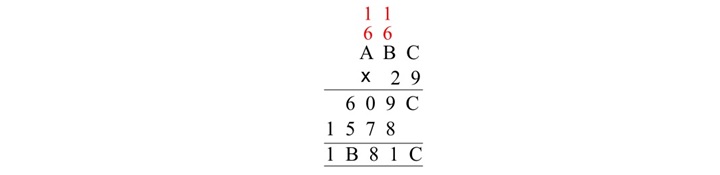
(ABC)16 乘以 (29)16 = (1B81C)16
解释
在此示例中,我们首先将第二个数字 (29)16 的数字 (9)16 乘以该数字的每个数字(ABC)16。记下部分积。
然后,我们将数字 (29)16 的数字 (2)16 乘以数字 (ABC)16 的每个数字。通过向左移动一位来记下部分积。
最后,我们将所有部分积相加以获得最终结果。
因此,(ABC)16 和 (29)16 的十六进制乘积为 (1B81C)16。
十六进制除法
十六进制除法是我们对 16 进制数字执行的第四个基本算术运算。在十六进制除法中,我们得到两个结果,即商和余数。
执行十六进制除法的步骤如下 −
- 步骤 1 − 从被除数的最左边的数字开始除法。
- 步骤 2 − 将得到的商乘以除数,然后从被除数中减去。
- 步骤 3 − 将被除数的下一位或多位有效数字去掉。
- 步骤 4 −重复上述三个步骤中说明的过程,直到被除数中的所有数字都用完为止。
以下示例演示了执行十六进制除法的过程。
示例 1
将 (A29)16 除以 (5)16。
解决方案
将 A29 除以 5 的十六进制除法如下所示 −
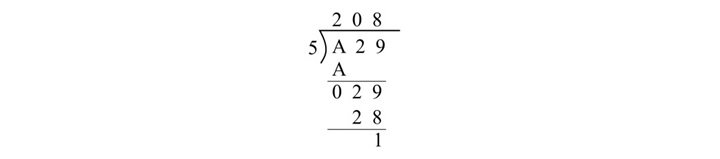
在此十六进制除法中,我们得到了商 (208)16 和余数 (1)16。
示例2
用 (1AC)16 除以 (A)16。
解决方案
给定数字的十六进制除法如下所示 −

在此示例中,我们得到了商 (2A)16 和余数 (8)16。
我们解释了执行十六进制算术运算的直接方法。现在让我们看看如何通过二进制算术执行所有这四个十六进制算术运算。
众所周知,每个十六进制数字可以表示为四位组,如下表所示。
| 十六进制 | 二进制 |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
现在我们来讨论一下通过二进制转换进行十六进制算术运算。
通过二进制转换进行十六进制加法
在这种将两个十六进制数相加的方法中,我们首先将它们转换为等效的二进制格式,然后使用二进制算术规则将得到的二进制数相加,最后将最终结果转换回十六进制格式。
以下示例演示了通过二进制转换进行十六进制加法的过程。
示例
通过二进制转换将 (A5C)16 和 (CCD)16 相加。
解决方案
将给定的十六进制数转换为等效的二进制数,
(A5C)16 = (1010 0101 1100)2
(CCD)16 = (1100 1100 1101)2
将得到的二进制数相加,

最后,将二进制和转换为其等效的十六进制格式以获得最终结果。
(0001 0111 0010 1001)2 = (1729)16
因此,十六进制和(A5C)16 和 (CCD)16 是 (1729)16。
通过二进制转换进行十六进制减法
要通过二进制转换减去两个十六进制数,我们首先将给定的十六进制数转换为其二进制等价数。然后,按照二进制算术规则减去它们。最后,将最终结果转换回十六进制格式。
以下示例演示了通过二进制转换进行十六进制减法的过程。
示例
使用二进制算术从 (FEA)16 中减去 (AC2)16。
解决方案
将给定的十六进制数转换为其二进制等价数,
(FEA)16 = (1111 1110 1010)2
(AC2)16 = (1010 1100 0010)2
减去获得的二进制数字,

将差值转换回十六进制以获得最终结果,
(0101 0010 1000)2 = (528)16
因此,(FEA)16 和 (AC2)16 的十六进制差值为 (528)16。
通过二进制转换进行十六进制乘法
我们还可以通过将两个十六进制数转换为其二进制等价数来将它们相乘。为此,我们首先将给定的十六进制数转换为其二进制等价数,然后按照二进制算术规则将二进制数相乘,并将结果转换回十六进制以获得最终结果。
以下示例演示了通过二进制转换将十六进制数相乘的过程。
示例
通过二进制转换将 (A9C)16 乘以 (B)16。
解决方案
将给定的十六进制数转换为其等效的二进制数,
(A9C)16 = (1010 1001 1100)2
(B)16 = (1011)2
将二进制数相乘,

将给定的十六进制数转换为其等效的二进制数,
(A9C)16 = (1010 1001 1100)2
将二进制数相乘,

将给定的十六进制数转换为其等效的二进制数,
乘积恢复为十六进制格式,(0111 0100 1011 0100)2 = (74B4)16
因此,A9C 和 B 的十六进制乘积为 74B4。
通过二进制转换进行十六进制除法
十六进制除法也可以使用二进制算术执行。在此方法中,我们首先将给定的十六进制数转换为其二进制等价数,然后按照二进制除法规则对其进行除法。最后,我们将结果从二进制格式转换为十六进制以获得最终结果。
让我们借助一个例子来理解使用二进制算术进行十六进制除法。
示例
使用二进制算术将 (AB8)16 除以 (A)16。
解决方案
将给定的十六进制数转换为其二进制等价数,
(AB8)16 = (1010 1011 1000)2
(A)16 = (1010)2
将获得的二进制除法数字,
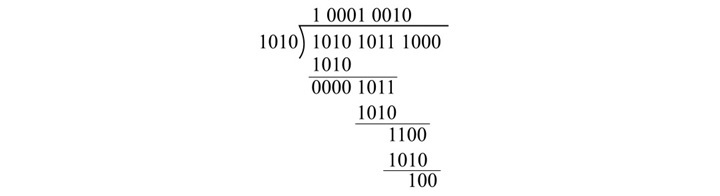
将商和余数转换为十六进制,
商 = (0001 0001 0010)2 = (112)16
余数 = (0100)2 = (4)16
结论
在本章中,我们解释了十六进制数的四种基本算术运算(加法、减法、乘法和除法)。我们还讨论了十六进制算术运算的二进制方法。

